2022年高中數(shù)學(xué) 第二講 直線與圓的位置關(guān)系 一 圓周角定理課后訓(xùn)練 新人教A版選修4-1

《2022年高中數(shù)學(xué) 第二講 直線與圓的位置關(guān)系 一 圓周角定理課后訓(xùn)練 新人教A版選修4-1》由會(huì)員分享，可在線閱讀，更多相關(guān)《2022年高中數(shù)學(xué) 第二講 直線與圓的位置關(guān)系 一 圓周角定理課后訓(xùn)練 新人教A版選修4-1（5頁珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

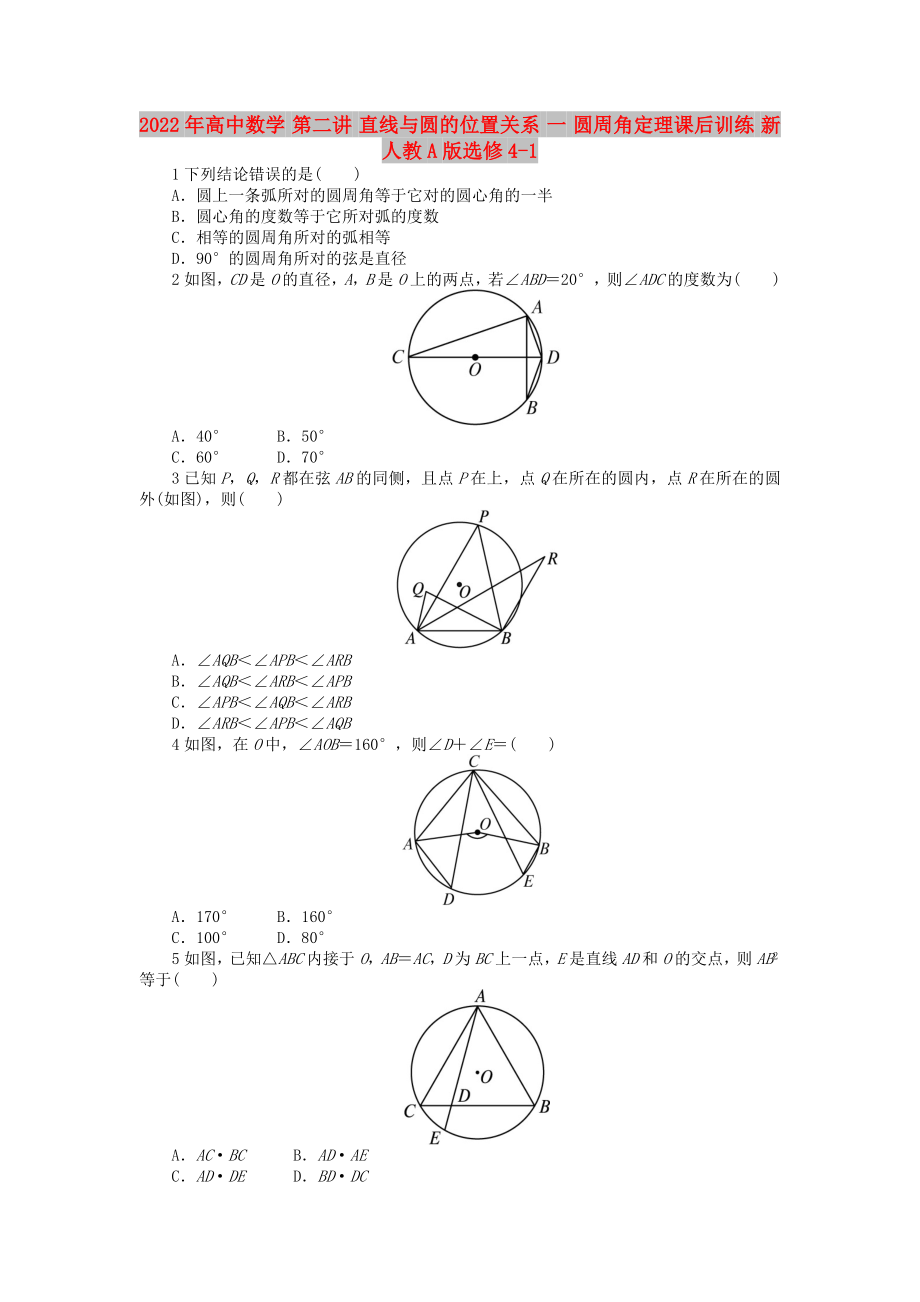
1、2022年高中數(shù)學(xué) 第二講 直線與圓的位置關(guān)系 一 圓周角定理課后訓(xùn)練 新人教A版選修4-1 1下列結(jié)論錯(cuò)誤的是(　　) A．圓上一條弧所對(duì)的圓周角等于它對(duì)的圓心角的一半 B．圓心角的度數(shù)等于它所對(duì)弧的度數(shù) C．相等的圓周角所對(duì)的弧相等 D．90°的圓周角所對(duì)的弦是直徑 2如圖，CD是O的直徑，A，B是O上的兩點(diǎn)，若∠ABD＝20°，則∠ADC的度數(shù)為(　　) A．40° B．50° C．60° D．70° 3已知P，Q，R都在弦AB的同側(cè)，且點(diǎn)P在上，點(diǎn)Q在所在的圓內(nèi)，點(diǎn)R在所在的圓外(如圖)，則(　　) A．∠AQB＜∠APB＜∠ARB B

2、．∠AQB＜∠ARB＜∠APB C．∠APB＜∠AQB＜∠ARB D．∠ARB＜∠APB＜∠AQB 4如圖，在O中，∠AOB＝160°，則∠D＋∠E＝(　　) A．170° B．160° C．100° D．80° 5如圖，已知△ABC內(nèi)接于O，AB＝AC，D為BC上一點(diǎn)，E是直線AD和O的交點(diǎn)，則AB2等于(　　) A．AC·BC 　　B．AD·AE C．AD·DE 　　D．BD·DC 6如圖，點(diǎn)A，B，C是圓O上的點(diǎn)，且∠ACB＝30°，則∠AOB等于____． 7AB是半圓O的直徑，點(diǎn)C在半圓上，CD⊥AB于點(diǎn)D，且AD＝3BD，則___

3、_______. 8如圖，AB為O的直徑，弦AC，BD交于點(diǎn)P，若AB＝3，CD＝1，則sin∠APD＝__________. 9如圖，O是△ABC的外接圓，D是的中點(diǎn)，BD交AC于點(diǎn)E. (1)求證：CD2＝DE·DB； (2)若CD＝，O到AC的距離為1，求O的半徑． 10(情景題)足球場上有句順口溜：“沖向球門跑，越近就越好；沿著球門跑，射點(diǎn)要選好．”可見踢足球是有“學(xué)問”的．如圖，在足球比賽中，甲、乙兩名隊(duì)員互相配合向?qū)Ψ角蜷TMN進(jìn)攻，當(dāng)甲帶球沖到A點(diǎn)時(shí)，乙已跟隨沖到B點(diǎn)，此時(shí)甲直接射門好，還是迅速將球回傳給乙，讓乙射門好？ 參考答案 1 答案：C　選項(xiàng)A

4、是圓周角定理；選項(xiàng)B是圓心角定理；選項(xiàng)D是圓周角定理的推論2；選項(xiàng)C中，缺少前提條件：在同圓或等圓中，故選C. 2答案：D　∵∠ABD＝∠ACD，∴∠ACD＝20°. 又CD是O的直徑，∴∠CAD＝90°. ∴∠ADC＝90°－∠ACD＝90°－20°＝70°. 3答案：D　如圖所示，延長AQ交圓O于點(diǎn)C，設(shè)AR與圓O相交于點(diǎn)D，連接BC，BD，則有∠AQB＞∠ACB，∠ADB＞∠ARB. 因?yàn)椤螦CB＝∠APB＝∠ADB， 所以∠AQB＞∠APB＞∠ARB. 4答案：C　如圖所示，連接CO， 則有∠AOC＋∠BOC＝360°－∠AOB＝360°－160°＝200°.

5、 又∠ADC＝∠AOC，∠BEC＝∠BOC， ∴∠ADC＋∠BEC＝(∠AOC＋∠BOC)＝100°，即∠D＋∠E＝100°. 5答案：B　如圖，連接BE. ∵AB＝AC， ∴∠ABC＝∠ACB. ∵∠ACB＝∠AEB， ∴∠ABC＝∠AEB. 又∵∠BAE＝∠DAB， ∴△ABD∽△AEB. ∴AB∶AE＝AD∶AB， 即AB2＝AD·AE. 6 答案：60°　∵∠ACB＝30°， ∴∠AOB＝2∠ACB＝60°. 7答案：　如圖，連接AC，BC，則 ∠ACB＝90°. 設(shè)BD＝k，則AD＝3k. ∵CD⊥AB， ∴CD2＝AD·BD＝3k2. ∴

6、CD＝k，∴. 8答案：　由于AB為O的直徑，則∠ADP＝90°， 所以△APD是直角三角形. 則sin∠APD＝，cos∠APD＝. 由題意知，∠DCP＝∠ABP，∠CDP＝∠BAP， 所以△PCD∽△PBA. 所以，又AB＝3，CD＝1，則. 所以cos∠APD＝. 又sin2∠APD＋cos2∠APD＝1， 所以sin∠APD＝. 9答案：分析：(1)轉(zhuǎn)化為證明△BCD與△CED相似； (2)作出點(diǎn)O到AC的距離，利用勾股定理列出方程求解. (1)證明：如圖，連接OD，OC，OD交AC于點(diǎn)F， 由已知，得∠ABD＝∠CBD. 又∵∠ECD＝∠ABD， ∴

7、∠CBD＝∠ECD. 又∵∠BDC＝∠CDE， ∴△BCD∽△CED. ∴，即CD2＝DE·DB. (2)解：連接OD交AC于點(diǎn)F，連接OC. ∵D是的中點(diǎn)，∴OD⊥AC，垂足為點(diǎn)F. 在Rt△CFO中，OF＝1，設(shè)O的半徑OC＝R， ∴. 在Rt△CFD中，DC2＝CF2+DF2. ∴＝(R2－1)+(R－1)2， 整理得R2－R－6＝0，解得R＝3或R＝－2(舍去)， ∴R＝3，即O的半徑為3. 10答案：分析：用數(shù)學(xué)方法從兩點(diǎn)的靜止的狀態(tài)來考慮.如果兩個(gè)點(diǎn)到球門的距離相差不大，要確定較好的射門位置，關(guān)鍵是看這兩點(diǎn)各自對(duì)球門MN的張角大小，當(dāng)張角較小時(shí)，容易被對(duì)方守門員攔截. 解：連接MB，MA，NA，NB，MA交圓于點(diǎn)C，連接NC， 則∠MBN＝∠MCN. 又∠MCN＞∠MAN， ∴∠MBN＞∠MAN. ∴甲應(yīng)該傳給乙，讓乙射門好.