《浙江省2022年中考數(shù)學(xué) 第七單元 圖形的變換測(cè)試練習(xí) (新版)浙教版》由會(huì)員分享��,可在線閱讀�����,更多相關(guān)《浙江省2022年中考數(shù)學(xué) 第七單元 圖形的變換測(cè)試練習(xí) (新版)浙教版(9頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
1��、浙江省2022年中考數(shù)學(xué) 第七單元 圖形的變換測(cè)試練習(xí) (新版)浙教版
一���、選擇題(每小題6分,共42分)
1.下列圖形中,既是軸對(duì)稱圖形又是中心對(duì)稱圖形的是 ( )
圖D7-1
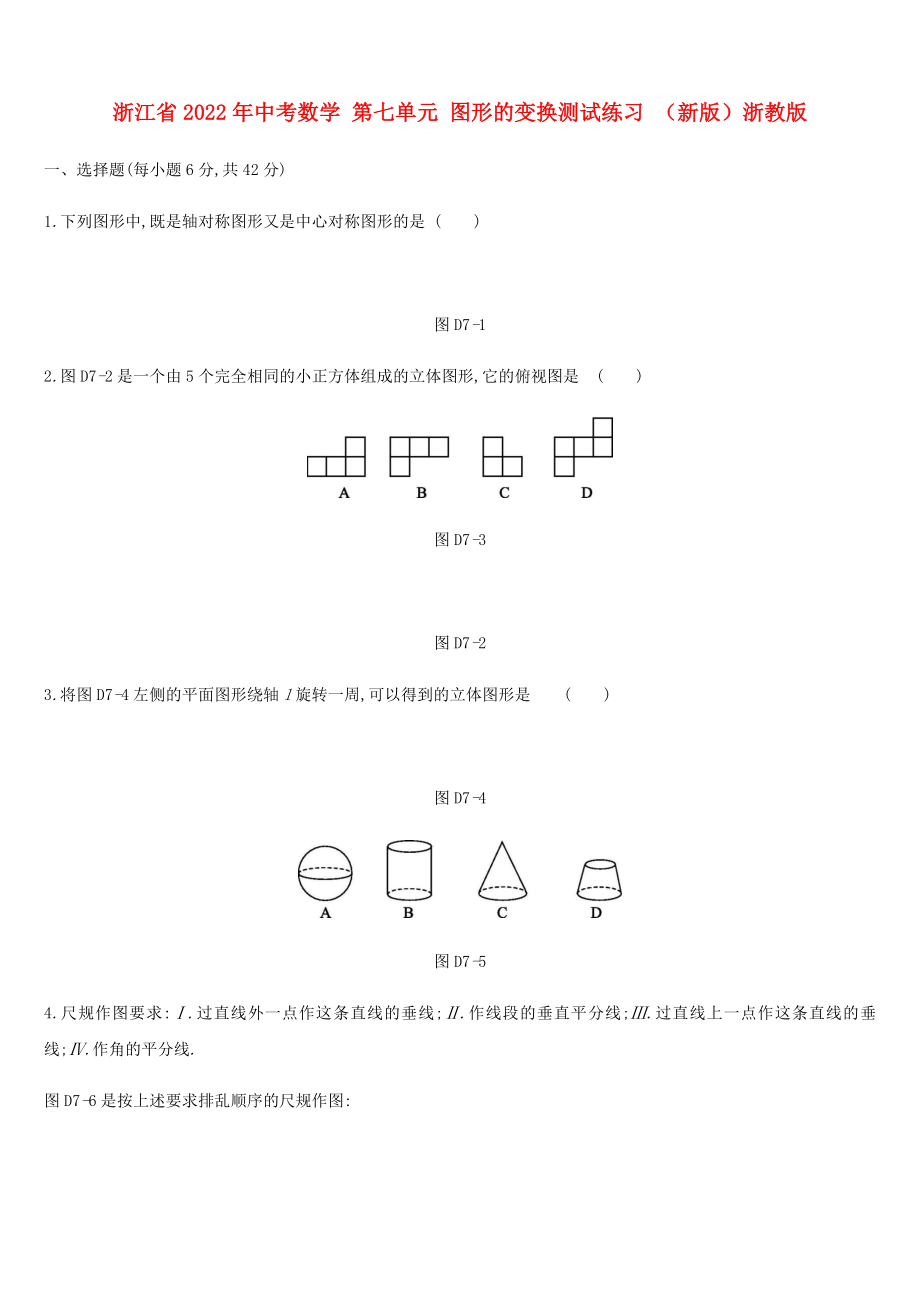
2.圖D7-2是一個(gè)由5個(gè)完全相同的小正方體組成的立體圖形,它的俯視圖是 ( )
圖D7-3
圖D7-2
3.將圖D7-4左側(cè)的平面圖形繞軸l旋轉(zhuǎn)一周,可以得到的立體圖形是 ( )
圖D7-4
圖D7-5
4.尺規(guī)作圖要求:Ⅰ.過直線外一點(diǎn)作這條直線的垂線;Ⅱ.作線段的垂直平分線;Ⅲ.過直線上一點(diǎn)作這條直線的垂線;Ⅳ.作角的平分線.
圖D7-6是按上述要求排亂順序的尺
2�、規(guī)作圖:
圖D7-6
則正確的配對(duì)是 ( )
A.①—Ⅳ,②—Ⅱ,③—Ⅰ,④—Ⅲ
B.①—Ⅳ,②—Ⅲ,③—Ⅱ,④—Ⅰ
C.①—Ⅱ,②—Ⅳ,③—Ⅲ,④—Ⅰ
D.①—Ⅳ,②—Ⅰ,③—Ⅱ,④—Ⅲ
5.圖D7-7是某圓錐的主視圖和左視圖,該圓錐的側(cè)面積是 ( )
圖D7-7
A.25π B.24π
C.20π D.15π
6.對(duì)角線長分別為6和8的菱形ABCD如圖D7-8所示,點(diǎn)O為對(duì)角線的交點(diǎn),過點(diǎn)O折疊菱形,使B,B'兩點(diǎn)重合,MN是折痕.若B'M=1,則CN的長為 ( )
圖D7-8
A.7 B.6
C.5 D.4
7.由若干個(gè)
3��、完全相同的小正方體組成一個(gè)立體圖形,它的左視圖和俯視圖如圖D7-9所示,則小正方體的個(gè)數(shù)不可能是( )
圖D7-9
A.5 B.6
C.7 D.8
二��、填空題(每小題6分,共24分)
8.如圖D7-10,在平面直角坐標(biāo)系中,A(4,0),B(0,3),以點(diǎn)A為圓心,AB長為半徑畫弧,交x軸的負(fù)半軸于點(diǎn)C,則點(diǎn)C坐標(biāo)為 .?
圖D7-10
9.如圖D7-11,在△ABC中,按以下步驟作圖:①分別以點(diǎn)A和點(diǎn)C為圓心,以大于AC的長為半徑作弧,兩弧相交于M,N兩點(diǎn);②作直線MN交BC于點(diǎn)D,連結(jié)AD.若AB=BD,AB=6,∠C=30°,則△ACD的面積為
4����、 .?
圖D7-11
10.如圖D7-12,在矩形ABCD中,AB=2,BC=4,點(diǎn)E,F分別在BC,CD上,若AE=,∠EAF=45°,則AF的長為 .
圖D7-12?
11.在Rt△ABC中,AB=1,∠A=60°,∠ABC=90°,如圖D7-13所示,將Rt△ABC沿直線l無滑動(dòng)地滾動(dòng)至Rt△DEF,則點(diǎn)B所經(jīng)過的路徑與直線l所圍成的封閉圖形的面積為 .(結(jié)果不取近似值)?
圖D7-13
三����、解答題(共34分)
12.(10分)如圖D7-14,矩形ABCD中,AB>AD,把矩形沿對(duì)角線AC所在直線折疊,使點(diǎn)B落在點(diǎn)E處,AE交CD于點(diǎn)F,連結(jié)
5����、DE.
(1)求證:△ADE≌△CED;
(2)求證:△DEF是等腰三角形.
圖D7-14
13.(12分)求證:相似三角形對(duì)應(yīng)邊上的中線之比等于相似比.
要求:(1)根據(jù)給出的△ABC及線段A'B',∠A'(∠A'=∠A),以線段A'B'為一邊,在給出的圖形上用尺規(guī)作出△A'B'C',使得△A'B'C'∽△ABC,不寫作法,保留作圖痕跡;
(2)在已有的圖形上畫出一組對(duì)應(yīng)中線,并據(jù)此寫出已知����、求證和證明過程.
圖D7-15
14.(12分)如圖D7-16,矩形ABCD中,AC=2AB,將矩形ABCD繞點(diǎn)A
6、旋轉(zhuǎn)得到矩形AB'C'D',使點(diǎn)B的對(duì)應(yīng)點(diǎn)B'落在AC上,B'C'交AD于點(diǎn)E,在B'C'上取點(diǎn)F,使B'F=AB.
(1)求證:AE=C'E;
(2)求∠FBB'的度數(shù);
(3)已知AB=2,求BF的長.
圖D7-16
參考答案
1.C 2.B
3.D [解析] A是由圓或半圓繞直徑旋轉(zhuǎn)一周得到的,故A錯(cuò)誤;B是由矩形繞其一邊旋轉(zhuǎn)一周得到的,故B錯(cuò)誤;C是由三角形繞一邊上的高旋轉(zhuǎn)一周得到的,故C錯(cuò)誤;D是由直角梯形繞軸l旋轉(zhuǎn)一周得到的,故D正確.
4.D [解析] 根據(jù)不同的作圖方法可以一一對(duì)應(yīng).②的已知點(diǎn)在直線外,所以對(duì)應(yīng)Ⅰ,④的已知點(diǎn)在直線上,所以對(duì)應(yīng)Ⅲ.
5.
7�、C [解析] 根據(jù)圓錐的主視圖、左視圖知,該圓錐的軸截面是一個(gè)底邊長為8,高為3的等腰三角形(如圖),
則AB==5,底面半徑=4,底面周長=8π,
∴側(cè)面積=×8π×5=20π,故選C.
6.D [解析] (法一,排除法)連結(jié)AC,BD,∵菱形ABCD,AC=6,BD=8,∴CO=3,DO=4,CO⊥DO,∴CD=5,而CN
8���、知曉俯視圖的第一行對(duì)應(yīng)左視圖的第一列,俯視圖的第二行對(duì)應(yīng)左視圖的第二列,所以,在俯視圖中,第一行至少有一個(gè)標(biāo)注數(shù)字2,最多有三個(gè)標(biāo)注數(shù)字2,第二行標(biāo)注1,所以小正方體的個(gè)數(shù)為1+1+1+1+2=6或1+1+1+2+2=7,1+1+2+2+2=8,不可能是5,故選A.
8.(-1,0)
9.9 [解析] 依題意MN是AC的垂直平分線,所以∠C=∠DAC=30°,所以∠ADB=∠C+∠DAC=60°,又AB=BD,所以△ABD為等邊三角形,∠BAD=60°,所以∠BAC=∠DAC+∠BAD=90°,因?yàn)锳B=6,所以AC=6,所以△ABC的面積為×6×6=18.又BD=AD=DC,所以S△AC
9���、D=S△ABC=9,故應(yīng)填9.
10. [解析] 取AD,BC的中點(diǎn)M,N,連結(jié)MN,由AD=4,AB=2,易得四邊形ABNM是正方形,連結(jié)EH(此處忽略EF,以免影響),由∠HAE=45°,四邊形ABNM是正方形,可知此處有典型的正方形內(nèi)“半角模型”,故有EH=MH+BE.由AB=2,AE=,易知BE=1,所以EN=BN-BE=2-1=1,設(shè)MH=x,由M是AD中點(diǎn),△AMH∽△ADF可知,DF=2MH=2x,HN=2-x,EH=MH+BE=x+1,在Rt△EHN中有EN2+HN2=EH2,故12+(2-x)2=(x+1)2,解得x=,故DF=,故AF==.
11.π+ [解析] 在
10、Rt△ABC中,AB=1,∠A=60°,∴BC=,∠BCB'=150°,∠B'A'E=120°.第一次滾動(dòng)的半徑為,根據(jù)扇形面積公式S扇形BCB'==,第二次滾動(dòng)的半徑為1,故S扇形B'A'E==,△ABC的面積為×1×=,所以總面積為++=+.
12.證明:(1)∵四邊形ABCD是矩形,
∴AD=BC,AB=CD.
由折疊的性質(zhì)可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中,
∴△ADE≌△CED(SSS).
(2)由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形.
11���、
13.解:(1)如圖所示,△A'B'C'就是所求作的三角形.
(2)已知:如圖,△A'B'C'∽△ABC,===k,A'D'=D'B',AD=DB,求證:=k.
證明:∵A'D'=D'B',AD=DB,
∴A'D'=A'B',AD=AB,
∴==.
∵△A'B'C'∽△ABC,
∴∠A=∠A',=,
在△A'D'C'和△ADC中,=,且∠A=∠A',
∴△A'D'C'∽△ADC,
∴==k.
14.[解析] (1)根據(jù)直角三角形直角邊和斜邊的關(guān)系,求出角的度數(shù);根據(jù)角之間關(guān)系,利用等角對(duì)等邊即可得證.
(2)利用旋轉(zhuǎn)前后對(duì)應(yīng)角相等���、對(duì)應(yīng)邊相等,從而得到等邊三角
12�、形,進(jìn)而求得角的度數(shù),再利用三角形內(nèi)角和是180°計(jì)算即可.
(3)連結(jié)AF,過點(diǎn)A作AM⊥BF于點(diǎn)M.易求∠AFM和∠ABM的度數(shù),然后利用三角函數(shù)求出BM和MF的長,再求出BF的長即可.
解:(1)證明:∵四邊形ABCD是矩形,
∴△ABC為直角三角形.
又∵AC=2AB,cos∠BAC==,
∴∠CAB=60°,
∴∠ACB=∠DAC=30°,∠B'AC'=60°,
∴∠C'AD=30°=∠AC'B',
∴AE=C'E.
(2)∵∠BAC=60°,又AB=AB',
∴△ABB'是等邊三角形,
∴BB'=AB,∠AB'B=60°.
又∵∠AB'F=90°,∴∠BB'F=150°.
∵B'F=AB=BB',
∴∠B'BF=∠BFB'=15°.
(3)連結(jié)AF,過點(diǎn)A作AM⊥BF于點(diǎn)M.
由(2)可知△AB'F是等腰直角三角形,△ABB'是等邊三角形.
∴∠AFB'=45°,∴∠AFM=30°,∠ABF=45°.
在Rt△ABM中,AM=BM=AB·cos∠ABM=2×=.
在Rt△AMF中,MF===.
∴BF=+.
 浙江省2022年中考數(shù)學(xué) 第七單元 圖形的變換測(cè)試練習(xí) (新版)浙教版
浙江省2022年中考數(shù)學(xué) 第七單元 圖形的變換測(cè)試練習(xí) (新版)浙教版