《安徽省銅陵市高中數(shù)學(xué) 第二章圓錐曲線與方程橢圓及其標(biāo)準(zhǔn)方程二學(xué)案無(wú)答案新人教A版選修21》由會(huì)員分享����,可在線閱讀�����,更多相關(guān)《安徽省銅陵市高中數(shù)學(xué) 第二章圓錐曲線與方程橢圓及其標(biāo)準(zhǔn)方程二學(xué)案無(wú)答案新人教A版選修21(7頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1��、
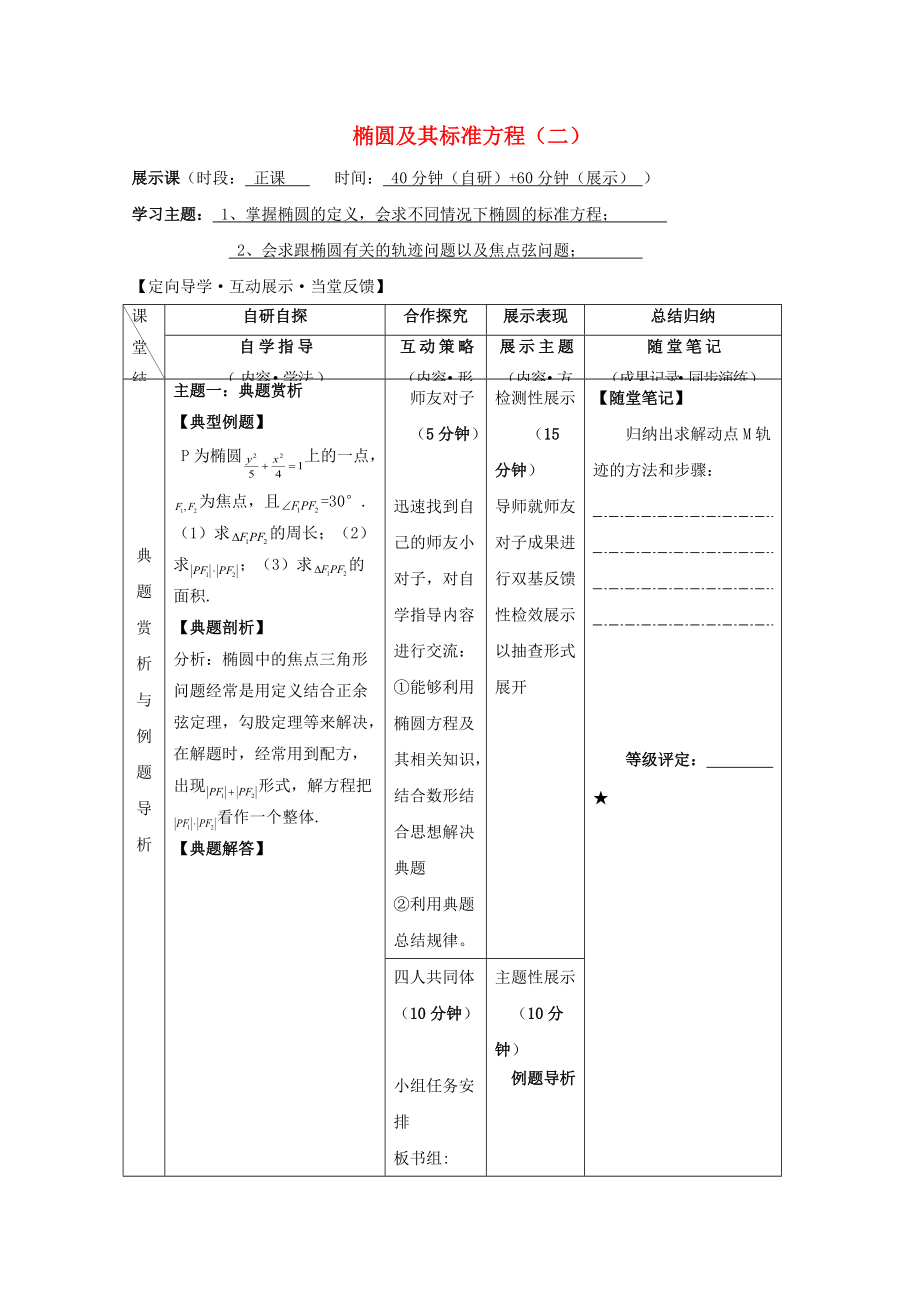
橢圓及其標(biāo)準(zhǔn)方程(二)
展示課(時(shí)段: 正課 時(shí)間: 40分鐘(自研)+60分鐘(展示) )
學(xué)習(xí)主題: 1��、掌握橢圓的定義��,會(huì)求不同情況下橢圓的標(biāo)準(zhǔn)方程����;
2、會(huì)求跟橢圓有關(guān)的軌跡問(wèn)題以及焦點(diǎn)弦問(wèn)題�����;
【定向?qū)W(xué)互動(dòng)展示當(dāng)堂反饋】
課堂
結(jié)構(gòu)
課程
結(jié)構(gòu)
自研自探
合作探究
展示表現(xiàn)
總結(jié)歸納
自 學(xué) 指 導(dǎo)
( 內(nèi)容學(xué)法 )
互 動(dòng) 策 略
(內(nèi)容形式)
展 示 主 題
(內(nèi)容方式)
隨 堂 筆 記
(成果記錄同步演練 )
典題賞析
與例題導(dǎo)析
2�����、主題一:典題賞析
【典型例題】
P為橢圓上的一點(diǎn)���,為焦點(diǎn)�,且=30.(1)求的周長(zhǎng)�����;(2)求;(3)求的面積.
【典題剖析】
分析:橢圓中的焦點(diǎn)三角形問(wèn)題經(jīng)常是用定義結(jié)合正余弦定理�,勾股定理等來(lái)解決,在解題時(shí)����,經(jīng)常用到配方,出現(xiàn)形式���,解方程把看作一個(gè)整體.
【典題解答】
師友對(duì)子
(5分鐘)
迅速找到自己的師友小對(duì)子����,對(duì)自學(xué)指導(dǎo)內(nèi)容進(jìn)行交流:
①能夠利用橢圓方程及其相關(guān)知識(shí)��,結(jié)合數(shù)形結(jié)合思想解決典題
②利用典題總結(jié)規(guī)律�����。
檢測(cè)性展示
(15分鐘)
導(dǎo)師就師友對(duì)子成果進(jìn)行雙基反饋性檢效展示
以抽查形式展開(kāi)
【隨堂筆記】
歸納出求解動(dòng)點(diǎn)M軌
3����、跡的方法和步驟:
等級(jí)評(píng)定: ★
四人共同體
(10分鐘)
小組任務(wù)安排
板書組:
組員在科研組長(zhǎng)帶領(lǐng)下安排1-2人進(jìn)行板書規(guī)劃����,其他同學(xué)互動(dòng)預(yù)展�����;
非板書組:
組員在科研組長(zhǎng)帶領(lǐng)下�����,進(jìn)行培輔與預(yù)展���;
主題性展示
(10分鐘)
例題導(dǎo)析
4、
?板書:例2�,例3;
?.展示例2�,例3,分析解題思慮��,總結(jié)求解方法和步驟
③用動(dòng)點(diǎn)坐標(biāo)表示斜率��,根據(jù)斜率之積為定值���,完成例3的學(xué)習(xí).�。
主題二:例題導(dǎo)析
自研課本文34頁(yè)(理41頁(yè))例2���,例3
自研教材例2�,例3的內(nèi)容思考下面問(wèn)題:
(1) 求軌跡問(wèn)題中,一般的我們?cè)O(shè)動(dòng)點(diǎn)M坐標(biāo)為(x�����,y),定點(diǎn)P坐標(biāo)為(x0�,y0),結(jié)合圖2.1-5�,說(shuō)出動(dòng)點(diǎn)與定點(diǎn)之間存在的等量關(guān)系?
(2)分析例2�,是如何用動(dòng)點(diǎn)M坐標(biāo)表示定點(diǎn)P坐標(biāo)的,并代入已知圓的方程��,可得到點(diǎn)M的軌跡.
(3)說(shuō)說(shuō)你能發(fā)現(xiàn)橢圓和圓之間有什么關(guān)系����?
(4) 針對(duì)(1),(2
5���、)請(qǐng)你總結(jié)出動(dòng)點(diǎn)M軌跡的求解步驟�����,記錄在隨堂筆記處.
(5)例題3中��,設(shè)動(dòng)點(diǎn)M的坐標(biāo)是(x����,y)���,請(qǐng)你用x,y分別表示出直線AM和直線BM的斜率.
40分鐘
同類演練
同類演練(15+2分鐘)
用1分鐘時(shí)間自主研讀下列題目���,并在作答區(qū)
(文)點(diǎn)p與定點(diǎn)F(2,0)的距離和它到定直線x=8的距離的比是1:2,求定點(diǎn)P的軌跡方程����,并說(shuō)明軌跡是什么圖形.
(理)已知橢圓的焦點(diǎn),點(diǎn)P在橢圓上����,若,則值為多少�?角度為多少?
【規(guī)范解題區(qū)】
課本頁(yè)練習(xí)答題區(qū)
6�����、
學(xué)習(xí)主題報(bào)告
主題:橢圓及其標(biāo)準(zhǔn)方程的相關(guān)題型及其解法
要求:1���、題材不限(框架圖�����、樹(shù)形圖�、思維導(dǎo)圖)
2、緊扣主題��,展示知識(shí)點(diǎn)���、可加題型�、可表困惑
� 高二 班 組 姓名: 滿分:100分 得分:
考查內(nèi)容:橢圓及其方程
考查主題:利用橢圓的相關(guān)知識(shí)解決問(wèn)題
考查形式:封閉式訓(xùn)練���,導(dǎo)師不指導(dǎo)���、不討論、不抄襲.
7�����、
溫馨提示:本次訓(xùn)練時(shí)間約為40分鐘�����,請(qǐng)同學(xué)們認(rèn)真審題,仔細(xì)答題�,安靜、自主的完成訓(xùn)練內(nèi)容.
基礎(chǔ)鞏固
1.橢圓的焦距是 ( )
A.2 B. C. D.
2.F1���、F2是定點(diǎn),|F1F2|=6�,動(dòng)點(diǎn)M滿足|MF1|+|MF2|=6,則點(diǎn)M的軌跡是( )
A.橢圓 B.直線 C.線段 D.圓
3.若橢圓的兩焦點(diǎn)為(-2�,0)和(2,0)���,且橢圓過(guò)點(diǎn)�����,
8���、則橢圓方程是( )
A. B.
C. D.
4.方程表示焦點(diǎn)在y軸上的橢圓,則k的取值范圍是( )
A. B.(0�����,2) C.(1�,+∞) D.(0��,1)
5. 已知<4���,則曲線和有( )
A. 相同的準(zhǔn)線 B. 相同的焦點(diǎn) C. 相同的離心率 D. 相同的長(zhǎng)軸
6.已知是橢圓上的一點(diǎn),若到橢圓右準(zhǔn)線的距離是�,則點(diǎn)到左焦點(diǎn)的距離是( ) ( )
A. B. C. D.
7.設(shè)定點(diǎn)F1(0,-3)�、F2(0,3)��,動(dòng)點(diǎn)P滿足條件���,則點(diǎn)P的軌跡是(
9����、 )
A.橢圓 B.線段 C.不存在 D.橢圓或線段
8.橢圓的一個(gè)焦點(diǎn)是��,那么等于( )
A. B. C. D.
9.橢圓內(nèi)有一點(diǎn)P(3����,2)過(guò)點(diǎn)P的弦恰好以P為中點(diǎn),那么這弦所在直線的方程為 ( )
A. B.
C. D.
10.平面內(nèi)有兩定點(diǎn)A�����、B及動(dòng)點(diǎn)P,設(shè)命題甲是:“|PA|+|PB|是定值”����,命題乙是:“點(diǎn)P的軌跡是以A.B為焦點(diǎn)的橢圓”,那么 ( )
A.甲是乙成立的充分不必要條件 B.甲是乙成立的必要不充分條件
C.甲
10�、是乙成立的充要條件 D.甲是乙成立的非充分非必要條件
11.橢圓上的點(diǎn)到直線的最大距離是 ( )
A.3 B. C. D.
發(fā)展提升
12.已知三角形的兩頂點(diǎn)為,它的周長(zhǎng)為,求頂點(diǎn)軌跡方程.
拓展提高
13.已知點(diǎn)A(0����,)和圓O1:x2+(y+)2=16�����,點(diǎn)M在圓O1上運(yùn)動(dòng)��,點(diǎn)P在半徑O1M上�,且|PM|=|PA|,求動(dòng)點(diǎn)P的軌跡方程.
6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375
 安徽省銅陵市高中數(shù)學(xué) 第二章圓錐曲線與方程橢圓及其標(biāo)準(zhǔn)方程二學(xué)案無(wú)答案新人教A版選修21
安徽省銅陵市高中數(shù)學(xué) 第二章圓錐曲線與方程橢圓及其標(biāo)準(zhǔn)方程二學(xué)案無(wú)答案新人教A版選修21