《云南省昭通市實(shí)驗(yàn)中學(xué)高中數(shù)學(xué)《第一章空間幾何體》同步練習(xí)新人教A必修》由會(huì)員分享���,可在線閱讀,更多相關(guān)《云南省昭通市實(shí)驗(yàn)中學(xué)高中數(shù)學(xué)《第一章空間幾何體》同步練習(xí)新人教A必修(12頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索�。
1、”云南省昭通市實(shí)驗(yàn)中學(xué)高中數(shù)學(xué)《第一章空間幾何體》同步練
習(xí)新人教A必修2"
�����、選擇題
1.
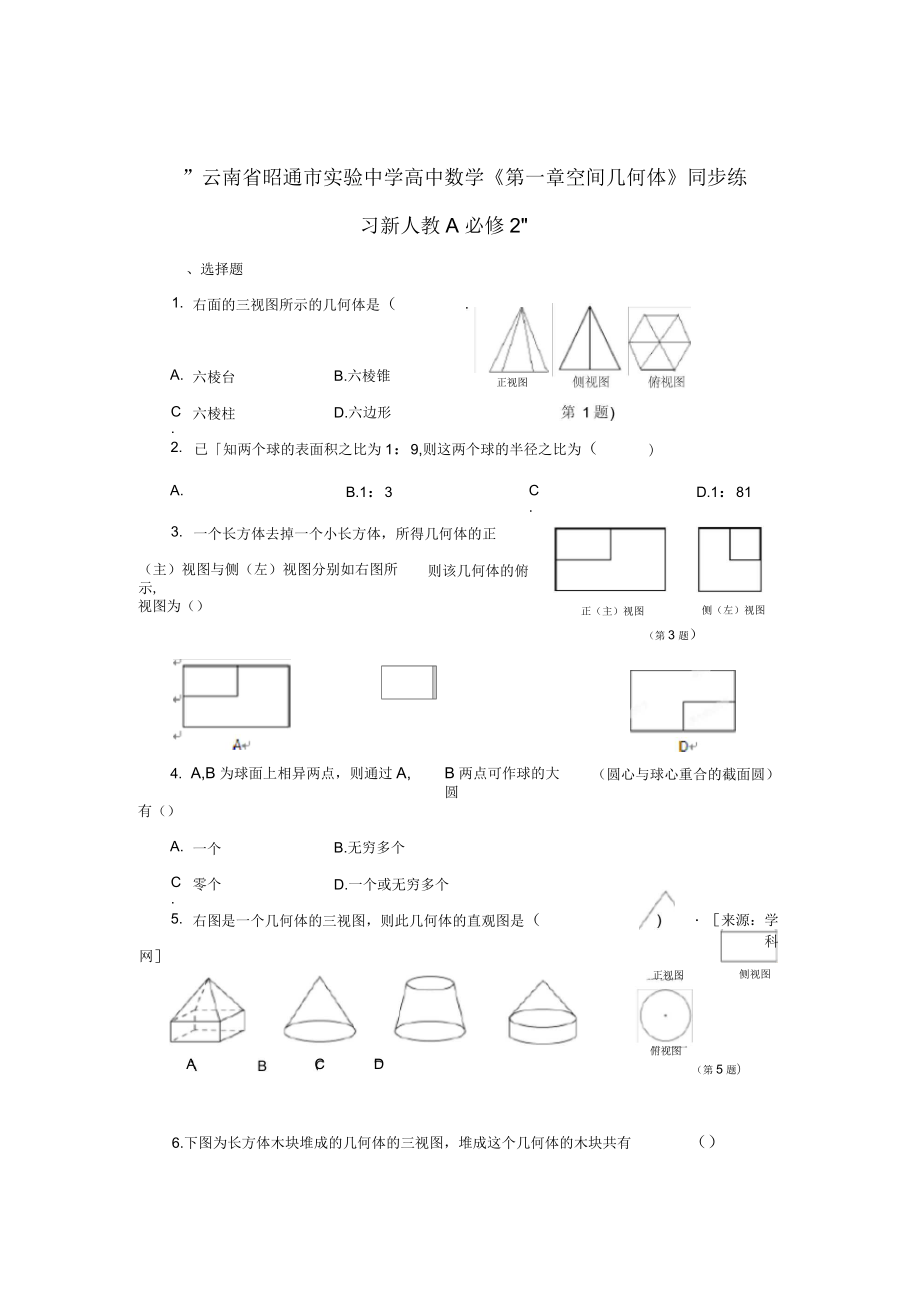
右面的三視圖所示的幾何體是(
A.
六棱臺(tái)
B.六棱錐
正視圖
C.
六棱柱
D.六邊形
)
2.
已「知兩個(gè)球的表面積之比為1:9,則這兩個(gè)球的半徑之比為(
A.
B.1:3
C.
D.1:81
3.
一個(gè)長方體去掉一個(gè)小長方體���,所得幾何體的正
(主)視圖與側(cè)(左)視圖分別如右圖所示,
則該幾何體的俯
正(主)視圖
側(cè)(左)視圖
視圖為()
4.
有()
A.
C.
5.
網(wǎng)]
(第3題)
A,B為球面上相異兩點(diǎn)�����,則通過A
2�、,
B兩點(diǎn)可作球的大圓
(圓心與球心重合的截面圓)
一個(gè)
零個(gè)
B.無窮多個(gè)
D.一個(gè)或無窮多個(gè)
右圖是一個(gè)幾何體的三視圖���,則此幾何體的直觀圖是(
正視圖
?[來源:學(xué)科
側(cè)視圖
C
A
D
俯視圖
(第5題)
6.下圖為長方體木塊堆成的幾何體的三視圖����,堆成這個(gè)幾何體的木塊共有 ()
A.
B.
C.
側(cè)覘田
(第6題)
D.
7.
3����、關(guān)于斜二測(cè)畫法畫直觀圖說法不正確的是
A.
在實(shí)物圖中取坐標(biāo)系不同���,所得的直觀圖有可能不同
B.
平行于坐標(biāo)軸的線段在直觀圖中仍然平行于坐標(biāo)軸
C.
平行于坐標(biāo)軸的線段長度在直觀.圖中仍然保持不變
D.
斜二測(cè)坐標(biāo)系取的角可能是135。
8.
如圖���,下列幾何體各自的三視圖中�,有且僅有兩個(gè)視圖相同的是
③三棱臺(tái)
④正四棱錐/
①正方體
②肆隹
A.①②
B.①③
C.①④
D.②④
9.一正方體的各頂點(diǎn)都在同一球面上,
用過球心的平面去截這個(gè)組合體�,截面圖不能
是(
A
10.如果一個(gè)三角形的平行投影仍然是
個(gè)三角形,則下列結(jié)論正確的是
A.原三
4����、角形的內(nèi)心的平行投影還是投影三角形的內(nèi)心
B.原三角形的重心的平行投影還是投影三角形的重心
C.原三角形的垂心的平行投影還是投影三角形的
「垂心
D.原三角形的外心的平行投影還是投影三角形的外心
二、填空題
11. 一圓球形氣球���,體積是8cm3,再打入一些空氣后�,氣球仍然保持為球形����,體積是
27cm3.則氣球半徑增加的百分率為.
12 .底面是菱形的棱柱
5、其側(cè)棱垂直于底面����,且側(cè)棱長為5,它的體對(duì)角線的長分別是
和15,則這個(gè)棱柱的側(cè)面積是.
13.右圖是一多面體的展開圖�,每個(gè)面內(nèi)都給了字母,
請(qǐng)根據(jù)要求回答問題:
①如果A是多面體的下底面,那么上面的面是
②如果面 F在前面���,從左邊看是面 B,那么上面的面
(第13題)
14. 一個(gè)幾何體的三視圖如下圖所示���,則此幾何體的體積是
三、解答題
15 .圓柱內(nèi)有一個(gè)四棱柱�,四棱柱的底面是圓柱底面的內(nèi)接正方形.已知圓柱表面積為
6,且底面圓直徑與母線長相等,求四棱柱的體積.
16 .下圖是一個(gè)幾何體的三視圖(單位:cm)�
(1)畫出這個(gè)幾何體的直觀圖(不要求寫畫法)
6�、;
(2)求這個(gè)幾何體的表面積及體積.
俯視圖
(第16題)
17.如圖�����,在四邊形
ABCD3, / DAB= 90 , / AD住 135 , AB= 5, CD= 2& �����, AD=
2,求四邊形 ABC啜直線AD旋轉(zhuǎn)一周所成幾何體的表面積及體積.
18 .已知正方體、球�����、底面直徑與母線相等的圓柱��,它們的表面積相等�,試比檢17端
體積V正方體)V球)V圓柱的大小.
19 .如圖,一個(gè)圓錐形容器的高為a,內(nèi)裝有一定量的水.如果將容器倒置��,這時(shí)水所
形成的圓錐的高恰為 -C,求原來水面的高度.
2
(第19題)
20 .如圖��,四棱柱的
7��、底面是菱形���,各側(cè)面都是長方形.兩個(gè)對(duì)角面也是長方形�����,面積分
別為Q,Q.求四棱柱的側(cè)面積.
��、選擇題
1.B
解析:由正視圖和側(cè)視圖可知幾何體為錐體�,由俯視圖可知幾何體為六棱錐.
2.A
解析:由設(shè)兩個(gè)球的半徑分別為r,R則4r2:4兀R=1:9.����,r2:R2=1:9,
即r:R=1:3.
3.C
解析:在根據(jù)得到三視圖的投影關(guān)系����,二.正視圖中小長方形位于左側(cè)����,,小長方形也位
于俯視圖「的左側(cè)��;二.小長方形位于側(cè)視圖的右側(cè)���,,小長方形一定位于俯視圖的下側(cè),
???圖C正確.
4.D
解析:A,B不在同一直徑的兩端點(diǎn)時(shí)��,過A,B兩點(diǎn)的大圓只有一個(gè)���;A,B在同一直
徑的
8、端點(diǎn)時(shí)大圓有無數(shù)個(gè).
5.D
解析:由幾何體的正視圖和側(cè)視圖可知�����,幾何體上部分為圓錐體,
由三個(gè)視圖可知幾何
體下部分為圓柱體,���,幾何體是由圓錐和圓柱組成的組合體.
6.D
解析:由三視圖可知幾何體為右圖所示�����,顯然組成幾何體的長方體木
塊有4塊.
7.C
解析:由平行于x軸和z軸的線段長度在直觀圖中仍然保持不變,
平行于y軸的線段長
度在直觀圖中是原來的一半��,�,C不對(duì).
8. D
解析:①的三個(gè)視圖
9、均相同���;②的正視圖和側(cè)視圖相同����;③的三個(gè)視圖均不相同;④的
正視圖和側(cè)視圖相同..??有且僅有兩個(gè)視圖相同的是②④.
9. A
解析:B是經(jīng)過正方體對(duì)角面的截面���;C是經(jīng)過球心且平行于正方體側(cè)面的截面���;D是
經(jīng)過一對(duì)平行的側(cè)面的中心,但不是對(duì)角面的截面.
10. B
解析:在平行投影中線段中點(diǎn)在投影后仍為中點(diǎn)�,故選B.
二、填空題
11. 50%
解析:設(shè)最初球的半徑為r,則8=4r3;打入空氣后的半徑為R,則27=-R3.
33
R3:r3=27:8.�,R:r=3:2.,氣球半徑增加的百分率為50%
12. 160.
解析:依條件得菱形底面對(duì)角線的長分別是,15252
10�����、=J200和』9252=<56.
,212P
�,菱形的邊長為]也叵叵���,空6=8.
丫2244
��,棱柱的側(cè)面積是5X4X8=160.
13. F,C.
解析:將多面體看成長方體�,A,F為相對(duì)側(cè)面.如果A是多面體的下底面����,那么上面的面是F;如果面F在前面��,從左邊看是面B,則右面看必是D,于是根據(jù)展開圖����,上面的面應(yīng)該是C.
14. 80.
解析:由三視圖可知����,幾何體是由棱長為4的正方體和底面邊長為4,高為3的四棱錐
組成,因此它的體積是V=43+-X42X3=64+16=80.
����、解答題
15. 參考答案:設(shè)圓柱底面圓半徑為r,則母線長為2r.
圓柱表面積為6,
6=2r2
11、+4r2.r=1.
四棱柱的底面是圓柱底面的內(nèi)接正方形,
正方形邊長為J2 .
四棱柱的體積 V= ( J2)2X2=2X2=4.
16 . (1)略.
(2)解:這個(gè)幾何體是三棱柱.
由于底面^ ABC勺BC邊上的高為1, BC= 2, AB= J2 .
故所求全面積 S>= 2Saabc+ Sbb���,c c+ 2Sabb A = 8+ 6='2 (cm2).
幾何體的體積 V= Sa ABC ? BB = lx2X1X3= 3(cm3).
2
17 .解:S表面=S下底面+ S臺(tái)側(cè)r面+S錐側(cè)面
=X52+ X(2 + 5)X5+ X 2X2 J2 = (60+4 J2
12��、)
V= V臺(tái)一 V錐=1 ( r12 +「1「2+ r22) h—1 r2h1 = 148 . 3 3 3
18 .解:設(shè)正方體的邊長為 a,球的半徑為r,圓柱的底面直徑為 2R
則 6a2= 4 兀 r 2= 6 兀 R2= S. a2= — , r2= — , R2= .
6 4兀 6冗
Q 3
(V 正方體)2= (a3) 2= (a2) 3=— 6
S3
216
2
2 4 3
(V干t) = - r
3
也兀2(r2)3=兀兀2
9 9
S3
108
(V圓柱)=(
兀 R2X2R)2
=4 兀 2(r2)3
S3
6兀 162
?
13���、?V正方體v;V圓柱〈V球.
19.解:設(shè)水形成的“圓臺(tái)”的上下底面半徑分別為r,R,高為h,則工=U
Ra�
則依條件得-hi-(r2+rR+R2)=2-a
332
-,化簡(jiǎn)得(h—a)3=— la3.
33
解得h=a-7a
即h=1紅a.
2
20.
解:設(shè)底面邊長為a,側(cè)棱長為l,
底面的兩對(duì)角線長分
別為c
d.
cl=Q1
dl=Q2
2
(第20題)
2d
Q2
2l
2
=a2.
2
由②得d=92,代入③得曳+
l2l
2la=,Q12+Q2.
故S側(cè)=4al=2JQ��;+Q2.
 云南省昭通市實(shí)驗(yàn)中學(xué)高中數(shù)學(xué)《第一章空間幾何體》同步練習(xí)新人教A必修
云南省昭通市實(shí)驗(yàn)中學(xué)高中數(shù)學(xué)《第一章空間幾何體》同步練習(xí)新人教A必修