《(人教通用)2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第17課時(shí) 解直角三角形知能優(yōu)化訓(xùn)練》由會(huì)員分享����,可在線閱讀,更多相關(guān)《(人教通用)2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第17課時(shí) 解直角三角形知能優(yōu)化訓(xùn)練(4頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1、第17課時(shí) 解直角三角形
知能優(yōu)化訓(xùn)練
中考回顧
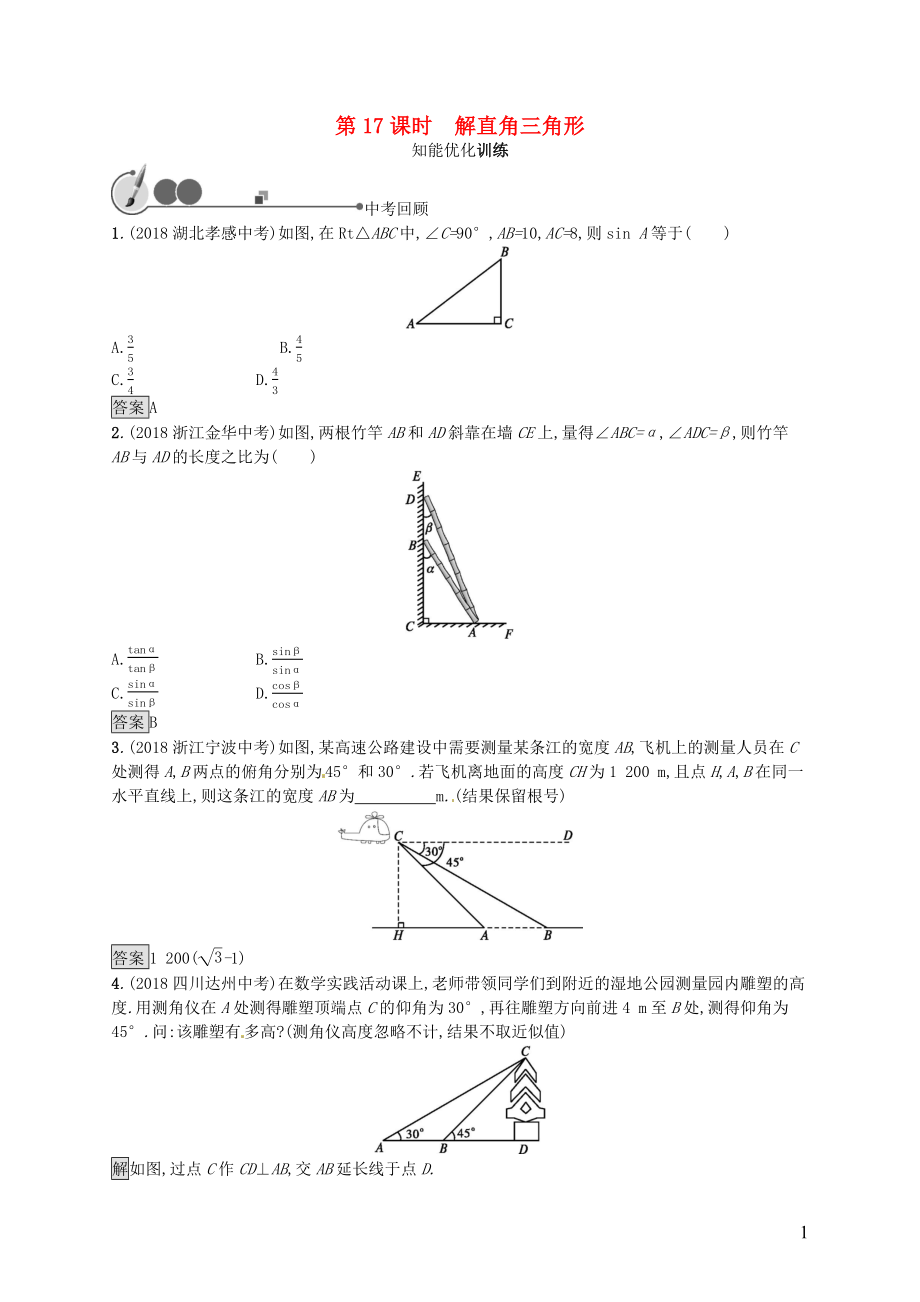
1.(2018湖北孝感中考)如圖,在Rt△ABC中,∠C=90°,AB=10,AC=8,則sin A等于( )
A.35 B.45
C.34 D.43
答案A
2.(2018浙江金華中考)如圖,兩根竹竿AB和AD斜靠在墻CE上,量得∠ABC=α,∠ADC=β,則竹竿AB與AD的長度之比為( )
A.tanαtanβ B.sinβsinα
C.sinαsinβ D.cosβcosα
答案B
3.(2018浙江寧波中考)如圖,某高速公路建設(shè)中需要測量某條江的寬度AB,飛機(jī)上的測量人員在C處測得A,B
2����、兩點(diǎn)的俯角分別為45°和30°.若飛機(jī)離地面的高度CH為1 200 m,且點(diǎn)H,A,B在同一水平直線上,則這條江的寬度AB為 m.(結(jié)果保留根號(hào))?
答案1 200(3-1)
4.(2018四川達(dá)州中考)在數(shù)學(xué)實(shí)踐活動(dòng)課上,老師帶領(lǐng)同學(xué)們到附近的濕地公園測量園內(nèi)雕塑的高度.用測角儀在A處測得雕塑頂端點(diǎn)C的仰角為30°,再往雕塑方向前進(jìn)4 m至B處,測得仰角為45°.問:該雕塑有多高?(測角儀高度忽略不計(jì),結(jié)果不取近似值)
解如圖,過點(diǎn)C作CD⊥AB,交AB延長線于點(diǎn)D.
設(shè)CD=xm.
∵∠CBD=45°,∠BDC=90°,∴BD=CD=xm.
∵∠A=30°,
3����、AD=AB+BD=(4+x)m,
∴tanA=CDAD,即33=x4+x,
解得x=2+23.
答:該雕塑的高度為(2+23)m.
5.(2018湖南衡陽中考)一名徒步愛好者來衡陽旅行,他從賓館C出發(fā),沿北偏東30°的方向行走2 000 m到達(dá)石鼓書院A處,參觀后又從A處沿正南方向行走一段距離,到達(dá)位于賓館南偏東45°方向的雁峰公園B處,如圖所示.
(1)求這臺(tái)徒步愛好者從石鼓書院走到雁峰公園的途中與賓館之間的最短距離;
(2)若這名徒步愛好者以100 m/min的速度從雁峰公園返回賓館,那么他在15 min內(nèi)能否到達(dá)賓館?
解(1)過點(diǎn)C作CP⊥AB于點(diǎn)P,
由題意可
4��、得∠A=30°,AC=2000m,
則CP=12AC=1000m.
即從石鼓書院走到雁峰公園的途中與賓館之間的最短距離為1000m.
(2)∵在Rt△PBC中,PC=1000m,∠PBC=∠BCP=45°,
∴BC=2PC=10002m.
∵這名徒步愛好者以100m/min的速度從雁峰公園返回賓館,
∴他到達(dá)賓館需要的時(shí)間為10002100=102<15,
∴他在15分鐘內(nèi)能到達(dá)賓館.
模擬預(yù)測
1.tan 60°的值等于( )
A.1 B.2
C.3 D.2
答案C
2.河堤橫斷面如圖,堤高BC=6 m,迎水坡AB的坡
5���、比為1∶3,則AB的長為( )
A.12 m B.43 m
C.53 m D.63 m
答案A
3.小明利用測角儀和旗桿的拉繩測量學(xué)校旗桿的高度.如圖,旗桿PA的高度與拉繩PB的長度相等.小明將PB拉到PB'的位置,測得∠PB'C=α(B'C為水平線),測角儀B'D的高度為1 m,則旗桿PA的高度為( )
A.11-sinα m B.11+sinα m
C.11-cosα m D.11+cosα m
答案A
4.如圖,在Rt△ABC中,∠ACB=90°,D是AB的中點(diǎn),過D點(diǎn)作AB的垂線交AC于點(diǎn)E,BC=6,sin A=35,則DE=.
答案
6�、154
5.如圖,某河堤的橫斷面是梯形ABCD,BC∥AD,迎水坡AB長為13 m,且tan∠BAE=125,則河堤的高BE為 m.?
答案12
6.如圖,某海監(jiān)船向正西方向航行,在A處望見一艘正在作業(yè)漁船D在南偏西45°方向,海監(jiān)船航行到B處時(shí)望見漁船D在南偏東45°方向,又航行了半小時(shí)到達(dá)C處,望見漁船D在南偏東60°方向,若海監(jiān)船的速度為50海里/時(shí),則A,B之間的距離為 .(取3≈1.7,結(jié)果精確到0.1海里)?
答案67.5海里
7.
如圖,小明在家里樓頂上的點(diǎn)A處,測量建在與小明家樓房同一水平線上相鄰的電梯樓的高,在點(diǎn)A處看電梯樓頂部點(diǎn)B
7�、處的仰角為60°,在點(diǎn)A處看這棟電梯樓底部點(diǎn)C處的俯角為45°,兩棟樓之間的距離為30 m,則電梯樓的高BC為 m.(結(jié)果精確到0.1 m,參考數(shù)據(jù):2≈1.414,3≈1.732)?
答案82.0
8.某商場為緩解“停車難”問題,擬建造地下停車庫,如圖是該地下停車庫坡道入口的設(shè)計(jì)示意圖,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根據(jù)規(guī)定,地下停車庫坡道入口上方要張貼限高標(biāo)志,以便告知駕駛員所駕車輛能否安全駛?cè)?小明認(rèn)為CD的長就是所限制的高度,而小亮認(rèn)為應(yīng)該
以CE的長作為限制的高度.小明和小亮誰說得對(duì)?請(qǐng)你判斷并計(jì)算出正確的結(jié)果.(結(jié)果精確到0.1 m,參考數(shù)據(jù):sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
解在△ABD中,∠ABD=90°,∠BAD=18°,BA=10,
∵tan∠BAD=BDBA,∴BD=10×tan18°.
∴CD=BD-BC=10×tan18°-0.5≈2.8(m).
在△ABD中,∠CDE=90°-∠BAD=72°.
∵CE⊥ED,∴∠DCE=18°.∴cos∠DCE=CECD.
∴CE=CD×cos∠CDE=2.8×cos18°≈2.7(m).
∵2.7m<2.8m,且CE⊥AE,∴小亮說得對(duì).
因此,小亮說得對(duì),CE為2.7m.
4
 (人教通用)2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第17課時(shí) 解直角三角形知能優(yōu)化訓(xùn)練
(人教通用)2019年中考數(shù)學(xué)總復(fù)習(xí) 第四章 幾何初步知識(shí)與三角形 第17課時(shí) 解直角三角形知能優(yōu)化訓(xùn)練