2018年高中數(shù)學(xué) 第三章 空間向量與立體幾何 3.2 空間向量在立體幾何中的應(yīng)用課件4 新人教B版選修2-1.ppt

《2018年高中數(shù)學(xué) 第三章 空間向量與立體幾何 3.2 空間向量在立體幾何中的應(yīng)用課件4 新人教B版選修2-1.ppt》由會(huì)員分享，可在線閱讀，更多相關(guān)《2018年高中數(shù)學(xué) 第三章 空間向量與立體幾何 3.2 空間向量在立體幾何中的應(yīng)用課件4 新人教B版選修2-1.ppt（16頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

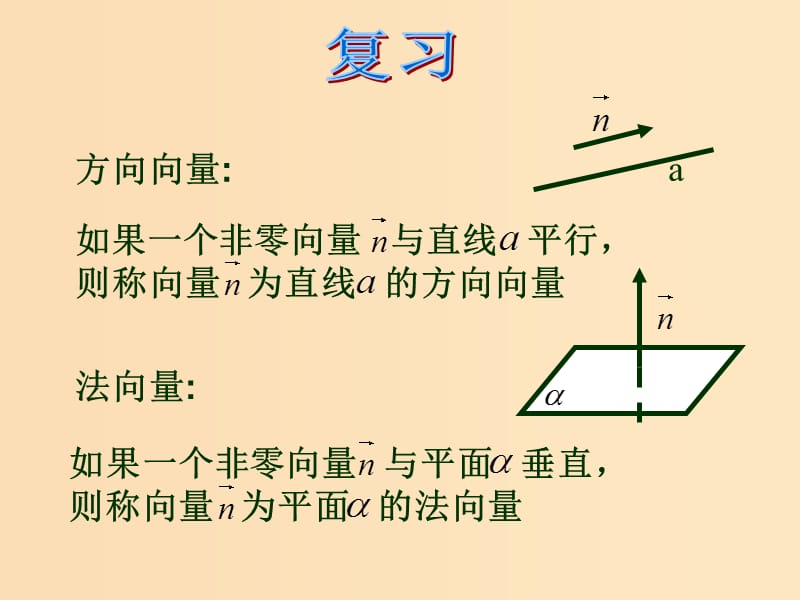
1、復(fù)習(xí),方向向量:,法向量:,如果一個(gè)非零向量 與直線 平行，則稱向量 為直線 的方向向量,如果一個(gè)非零向量 與平面 垂直，則稱向量 為平面 的法向量,,,復(fù)習(xí),,,,,例3如圖，已知長(zhǎng)方體 直線 與平面 所成的角為 ， 垂直 于 ， 為 的中點(diǎn).,（I）求異面直線AE與BF所成角的余弦值。 （II）求平面BDF與平面AA1B所成二面角的余弦值。,2,1,,,,,,,例3 如圖，已知長(zhǎng)方體 直線 與平面 所成的角為 ， 垂直 于 ， 為 的中點(diǎn)。,,,,,與平面 所成的角為,解：如圖，以A為原點(diǎn)，建立空間直角坐標(biāo)系A(chǔ)-xyz,2,1,x,z,y,,

2、,,,,,,,,,A(0,0,0),B(2,0,0),E( , ,0),例3 如圖，已知長(zhǎng)方體 直線 與平面 所成的角為 ， 垂直 于 ， 為 的中點(diǎn)。,（I）求異面直線AE與BF所成角的余弦值。,分析:即求 與 夾角余弦值的絕對(duì)值,F (1, 0,1),,,,,（I）求異面直線AE與BF所成角的余弦值。,,異面直線AE、BF 所成角的余弦值為,,,,B(2,0,0),D(0, ,0),（II）求平面BDF與平面AA1B所成二面角的余弦值。,F (1, 0,1),,,,,,,,令x=1得,所以平面BDF與平面AA1B所成二面角的余弦值為,由圖可知平面BDF與平面AA1

3、B所成二面角為銳角,（II）求平面BDF與平面AA1B所成二面角的余弦值。,如圖所示，在正方體ABCD-A1B1C1D1中，邊長(zhǎng)為2，M、N分別是A1B1 、B1B的中點(diǎn)， （1）求異面直線A1B、AC所成的角。 （2）求二面角B1-A1B-C1的余弦值。,變式訓(xùn)練,A(2,0,0),A1(2,0,2),B(2,2,0),解:如圖,以D為原點(diǎn), 建立空間直角坐標(biāo)系D-xyz,C(0,2,0),如圖所示，在正方體ABCD-A1B1C1D1中，邊長(zhǎng)為2，M、N分別是A1B1 、B1B的中點(diǎn)，,（1）求異面直線A1B、AC所成的角。,分析:可由 與 夾角余弦值的絕對(duì)值求得,如圖所示，在正方體AB

4、CD-A1B1C1D1中，邊長(zhǎng)為2，M、N分別是A1B1 、B1B的中點(diǎn)，,（1）求異面直線A1B、AC所成的角。,設(shè)異面直線A1B、AC所成的角為,如圖所示，在正方體ABCD-A1B1C1D1中，邊長(zhǎng)為2，M、N分別是A1B1 、B1B的中點(diǎn)，,（2）求二面角B1-A1B-C1的余弦值。,設(shè)平面A1BC1的法向量為,令z=1得：,A1(2,0,2),B(2,2,0),C1(0,2,2),（2）求二面角B1-A1B-C1的余弦值。,如圖所示，在正方體ABCD-A1B1C1D1中，邊長(zhǎng)為2，M、N分別是A1B1 、B1B的中點(diǎn)，,平面A1BC1的法向量為,二面角B1-A1B-C1的余弦值為,由圖可知:二面角B1-A1B-C1為銳角,小結(jié),1、求異面直線所成的角 2、求二面角,今天學(xué)習(xí)的主要內(nèi)容是什么?,作業(yè)： 如圖，在椎體P-ABCD中，ABCD是邊長(zhǎng)為1的棱形，且DAB=60， ,PB=2,E,F分別是BC,PC的中點(diǎn) （1） 證明：AD 平面DEF； （2） 求二面角P-AD-B的余弦值。,（2011年廣東高考）,謝謝,