【南方新課堂】高考新課標(biāo)數(shù)學(xué)文二輪專題復(fù)習(xí)檢測(cè)：專題四第1講空間幾何體的計(jì)算問題 Word版含解析

《【南方新課堂】高考新課標(biāo)數(shù)學(xué)文二輪專題復(fù)習(xí)檢測(cè)：專題四第1講空間幾何體的計(jì)算問題 Word版含解析》由會(huì)員分享，可在線閱讀，更多相關(guān)《【南方新課堂】高考新課標(biāo)數(shù)學(xué)文二輪專題復(fù)習(xí)檢測(cè)：專題四第1講空間幾何體的計(jì)算問題 Word版含解析（8頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

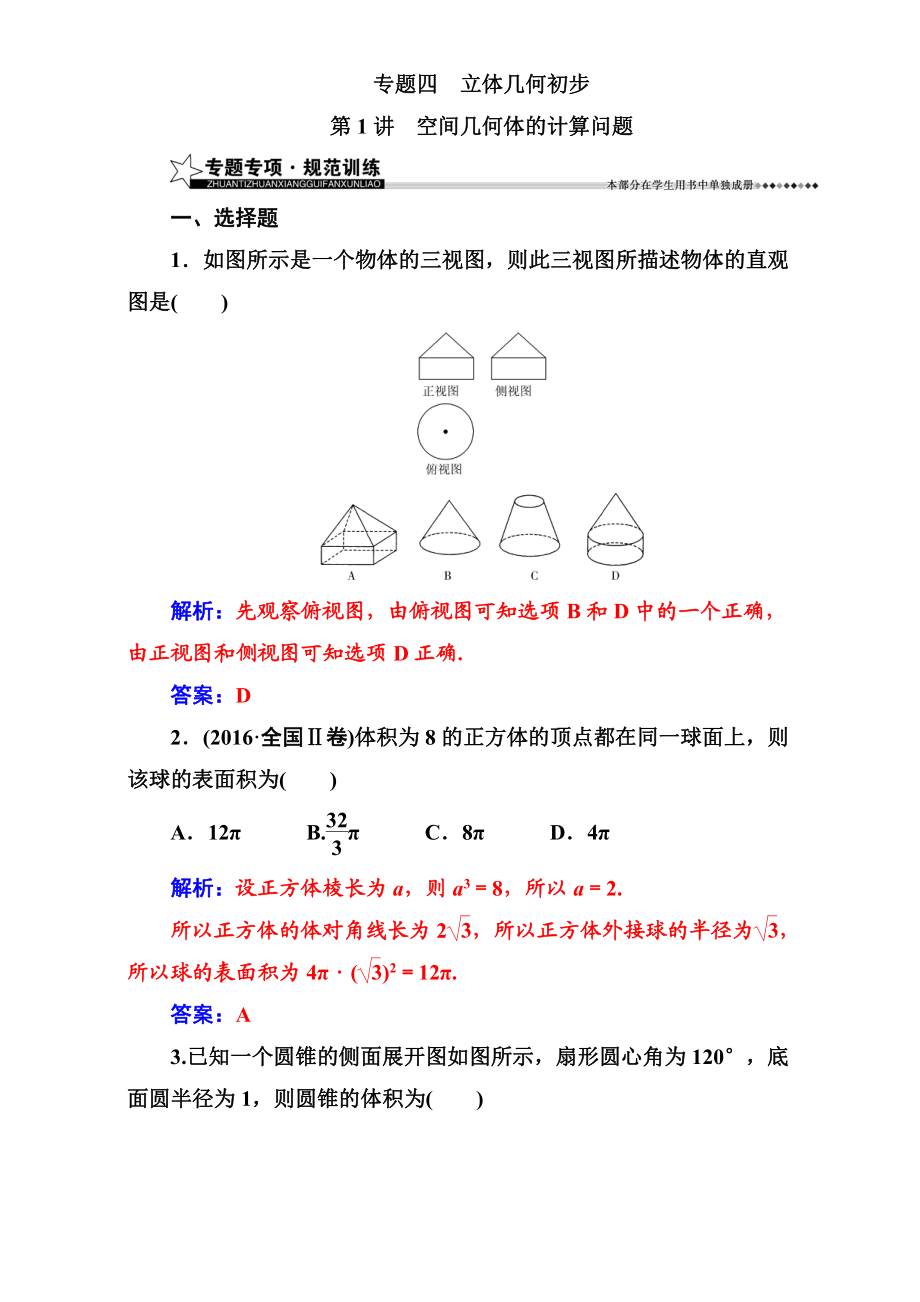
1、專題四專題四立體幾何初步立體幾何初步第第 1 講講空間幾何體的計(jì)算問題空間幾何體的計(jì)算問題一、選擇題一、選擇題1如圖所示是一個(gè)物體的三視圖如圖所示是一個(gè)物體的三視圖，則此三視圖所描述物體的直觀則此三視圖所描述物體的直觀圖是圖是()解析：解析：先觀察俯視圖先觀察俯視圖，由俯視圖可知選項(xiàng)由俯視圖可知選項(xiàng) B 和和 D 中的一個(gè)正確中的一個(gè)正確，由正視圖和側(cè)視圖可知選項(xiàng)由正視圖和側(cè)視圖可知選項(xiàng) D 正確正確答案：答案：D2(2016全國(guó)全國(guó)卷卷)體積為體積為 8 的正方體的頂點(diǎn)都在同一球面上的正方體的頂點(diǎn)都在同一球面上，則則該球的表面積為該球的表面積為()A12B.323C8D4解析：解析：設(shè)正方體

2、棱長(zhǎng)為設(shè)正方體棱長(zhǎng)為 a，則，則 a38，所以所以 a2.所以正方體的體對(duì)角線長(zhǎng)為所以正方體的體對(duì)角線長(zhǎng)為 2 3，所以正方體外接球的半徑為所以正方體外接球的半徑為 3，所以球的表面積為所以球的表面積為 4( 3)212.答案：答案：A3.已知一個(gè)圓錐的側(cè)面展開圖如圖所示已知一個(gè)圓錐的側(cè)面展開圖如圖所示，扇形圓心角為扇形圓心角為 120，底底面圓半徑為面圓半徑為 1，則圓錐的體積為則圓錐的體積為()A.2 23B. 2C.4 23D.5 23解析：解析：設(shè)底面半徑為設(shè)底面半徑為 r，母線母線 PB 長(zhǎng)為長(zhǎng)為 l，則弧長(zhǎng)則弧長(zhǎng) BC132l，又又弧長(zhǎng)弧長(zhǎng) BC2r2，所以所以132l2，l3，所

3、以所以 PO PB2OB2912 2，故圓錐的體積故圓錐的體積 V13r2h1312 22 23.答案：答案：A4(2016山東卷山東卷)一個(gè)由半球和四棱錐組成的幾何體一個(gè)由半球和四棱錐組成的幾何體，其三視圖如其三視圖如圖所示圖所示，則該幾何體的體積為則該幾何體的體積為()(導(dǎo)學(xué)號(hào)導(dǎo)學(xué)號(hào) 53130123)A.1323B.1323C.1326D126解析：解析：由三視圖知該四棱錐是底面邊長(zhǎng)為由三視圖知該四棱錐是底面邊長(zhǎng)為 1，高為高為 1 的正四棱錐的正四棱錐，結(jié)合三視圖可得半球半徑為結(jié)合三視圖可得半球半徑為22，從而該幾何體的體積為從而該幾何體的體積為1312112432231326.答案：

4、答案：C5(2016廣東汕頭模擬廣東汕頭模擬)某幾何體的三視圖如圖所示某幾何體的三視圖如圖所示，則該幾何體則該幾何體外接球的表面積為外接球的表面積為()A4 3B12C24D48解析：解析：由三視圖可知該幾何體為三棱錐由三視圖可知該幾何體為三棱錐 P-ABC，其中其中，PA平平面面ABC，ABBC，PAABBC2，取取 PC 的中點(diǎn)的中點(diǎn) O，AC 的中點(diǎn)的中點(diǎn) D，連接連接 OA，OD，BD，OB，則則 AC AB2BC22 2，則則 PC PA2AC22 3.OPOC 3，OA12PC 3，BD12AC 2，OD12PA1.易知易知 OD平面平面 ABC，OB OD2BD2 3，OAOBO

5、COP，O 是三棱錐是三棱錐 P-ABC 外接球的球心外接球的球心，外接球半徑外接球半徑 rOA 3，該幾何體外接球的表面積該幾何體外接球的表面積 S4r212.答案：答案：B二、填空題二、填空題6(2016北京卷北京卷)某四棱柱的三視圖如圖所示某四棱柱的三視圖如圖所示，則該四棱柱的體積則該四棱柱的體積為為_解析解析：由題意知該四棱柱為直四棱柱由題意知該四棱柱為直四棱柱，其高為其高為 1，其底面為上底長(zhǎng)其底面為上底長(zhǎng)為為 1，下底長(zhǎng)為下底長(zhǎng)為 2，高為高為 1 的等腰梯形的等腰梯形，所以該四棱柱的體積為所以該四棱柱的體積為 V（12）12132.答案：答案：327一個(gè)六棱錐的體積為一個(gè)六棱錐的

6、體積為 2 3，其底面是邊長(zhǎng)為其底面是邊長(zhǎng)為 2 的正六邊形的正六邊形，側(cè)，側(cè)棱長(zhǎng)都相等，則該六棱錐的側(cè)面積為棱長(zhǎng)都相等，則該六棱錐的側(cè)面積為_解析：解析：設(shè)棱錐的高為設(shè)棱錐的高為 h，則則 V13S底底h1363422h2 3，h1，由勾股定理知由勾股定理知，側(cè)棱長(zhǎng)為側(cè)棱長(zhǎng)為 2212 5.六棱錐六個(gè)側(cè)面全等六棱錐六個(gè)側(cè)面全等，且側(cè)面三角形的高為且側(cè)面三角形的高為 （ 5）2122，S側(cè)側(cè)1222612.答案：答案：128(2016浙江卷浙江卷)某幾何體的三視圖如圖所示某幾何體的三視圖如圖所示(單位：?jiǎn)挝唬篶m)，則該幾則該幾何體的表面積是何體的表面積是_cm2，體積是體積是_cm3.解析解

7、析：由三視圖還原幾何由三視圖還原幾何體如圖所示體如圖所示，下面長(zhǎng)方體的長(zhǎng)下面長(zhǎng)方體的長(zhǎng)、寬都是寬都是 4，高為高為 2；上面正方體的棱長(zhǎng)為；上面正方體的棱長(zhǎng)為 2.所以該幾何體的表面積為所以該幾何體的表面積為(442424)222480(cm2)；體積為；體積為 4422340(cm3)答案：答案：8040三、解答題三、解答題9(2015全國(guó)全國(guó)卷卷)如圖如圖，長(zhǎng)方體長(zhǎng)方體 ABCD-A1B1C1D1中中，AB16，BC10，AA18，點(diǎn)點(diǎn) E，F(xiàn) 分別在分別在 A1B1，D1C1上上，A1ED1F4.過過點(diǎn)點(diǎn)E，F(xiàn) 的平面的平面與此長(zhǎng)方體的面相交與此長(zhǎng)方體的面相交，交線圍成一個(gè)正方形交線圍成

8、一個(gè)正方形(導(dǎo)學(xué)號(hào)導(dǎo)學(xué)號(hào) 53130124)(1)在圖中畫出這個(gè)正方形在圖中畫出這個(gè)正方形(不必說明畫法和理由不必說明畫法和理由)；(2)求平面求平面把該長(zhǎng)方體分成的兩部分體積的比值把該長(zhǎng)方體分成的兩部分體積的比值解：解：(1)交線圍成的正方形交線圍成的正方形 EHGF 如圖所示如圖所示(2)作作 EMAB，垂足為垂足為 M，則則 AMA1E4，EB112，EMAA18.四邊形四邊形 EHGF 為正方形為正方形，EHEFBC10.于是于是 MH EH2EM26，故故 AH10，HB6.故故 S 四邊形四邊形 A1EHA12(410)856，S 四邊形四邊形 EB1BH12(126)872.長(zhǎng)方

9、體被平面長(zhǎng)方體被平面分成兩個(gè)高為分成兩個(gè)高為 10 的直棱柱的直棱柱，其積體的比值為其積體的比值為9779也正確也正確.10已知一個(gè)圓錐的底面半徑為已知一個(gè)圓錐的底面半徑為 R，高為高為 H，在其內(nèi)部有一個(gè)高在其內(nèi)部有一個(gè)高為為x 的內(nèi)接圓柱的內(nèi)接圓柱(1)求圓柱的側(cè)面積；求圓柱的側(cè)面積；(2)x 為何值時(shí)為何值時(shí)，圓柱的側(cè)面積最大？圓柱的側(cè)面積最大？解：解：(1)作圓錐的軸截面作圓錐的軸截面，如圖所示如圖所示rRHxH，rRRHx，S圓柱側(cè)圓柱側(cè)2rx2Rx2RHx2(0 xH)(2)2RH0，當(dāng)當(dāng) x2R4RHH2時(shí)時(shí)，S圓柱側(cè)圓柱側(cè)最大最大故當(dāng)故當(dāng) xH2，即圓柱的高為圓錐高的一半時(shí)即圓

10、柱的高為圓錐高的一半時(shí)，圓柱的側(cè)面積最大圓柱的側(cè)面積最大11(2016全國(guó)全國(guó)卷卷)如圖如圖，已知正三棱錐已知正三棱錐 P-ABC 的側(cè)面是直角三的側(cè)面是直角三角形角形，PA6，頂點(diǎn)頂點(diǎn) P 在平面在平面 ABC 內(nèi)的正投影為點(diǎn)內(nèi)的正投影為點(diǎn) D，D 在平面在平面 PAB內(nèi)的正投影為點(diǎn)內(nèi)的正投影為點(diǎn) E，連接連接 PE 并延長(zhǎng)交并延長(zhǎng)交 AB 于點(diǎn)于點(diǎn) G.(導(dǎo)學(xué)號(hào)導(dǎo)學(xué)號(hào) 53130125)(1)證明：證明：G 是是 AB 的中點(diǎn)；的中點(diǎn)；(2)在圖中作出點(diǎn)在圖中作出點(diǎn) E 在平面在平面 PAC 內(nèi)的正投影內(nèi)的正投影 F(說明作法及理由說明作法及理由)，并求四面體并求四面體 P-DEF 的體積

11、的體積(1)證明證明：P 在平面在平面 ABC 內(nèi)的正投影為內(nèi)的正投影為 D，ABPD.D 在平面在平面 PAB 內(nèi)的正投影為內(nèi)的正投影為 E，ABDE.PDDED，AB平面平面 PED，故故 ABPG.又由已知可得又由已知可得，PAPB，G 是是 AB 的中點(diǎn)的中點(diǎn)(2)解解：在平面在平面 PAB 內(nèi)內(nèi)，過點(diǎn)過點(diǎn) E 作作 PB 的平行線交的平行線交 PA 于點(diǎn)于點(diǎn) F，F(xiàn) 即即為為 E 在平面在平面 PAC 內(nèi)的正投影內(nèi)的正投影理由如下：由已知可得理由如下：由已知可得 PBPA，PBPC，又又 EFPB，EFPA，EFPC.又又 PAPCP，因此因此 EF平面平面 PAC，即點(diǎn)即點(diǎn) F 為

12、為 E 在平面在平面 PAC 內(nèi)的正投影內(nèi)的正投影連接連接 CG，P 在平面在平面 ABC 內(nèi)的正投影為內(nèi)的正投影為 D，D 是正三角形是正三角形 ABC 的中心的中心由由(1)知知，G 是是 AB 的中點(diǎn)的中點(diǎn)，D 在在 CG 上上，故故 CD23CG.由題設(shè)可得由題設(shè)可得 PC平面平面 PAB，DE平面平面 PAB，DEPC，因此因此 PE23PG，DE13PC.由已知由已知，正三棱錐的側(cè)面是直角三角形且正三棱錐的側(cè)面是直角三角形且 PA6，可得可得 DE2，PE2 2.在等腰直角三角形在等腰直角三角形 EFP 中中，可得可得 EFPF2，四面體四面體 P-DEF 的體積的體積 V131222243.