《（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 小專題（五）圓中常用的思想方法習(xí)題 （新版）滬科版》由會(huì)員分享，可在線閱讀，更多相關(guān)《（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 小專題（五）圓中常用的思想方法習(xí)題 （新版）滬科版（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、
小專題（五） 圓中常用的思想方法
類型1 方程思想
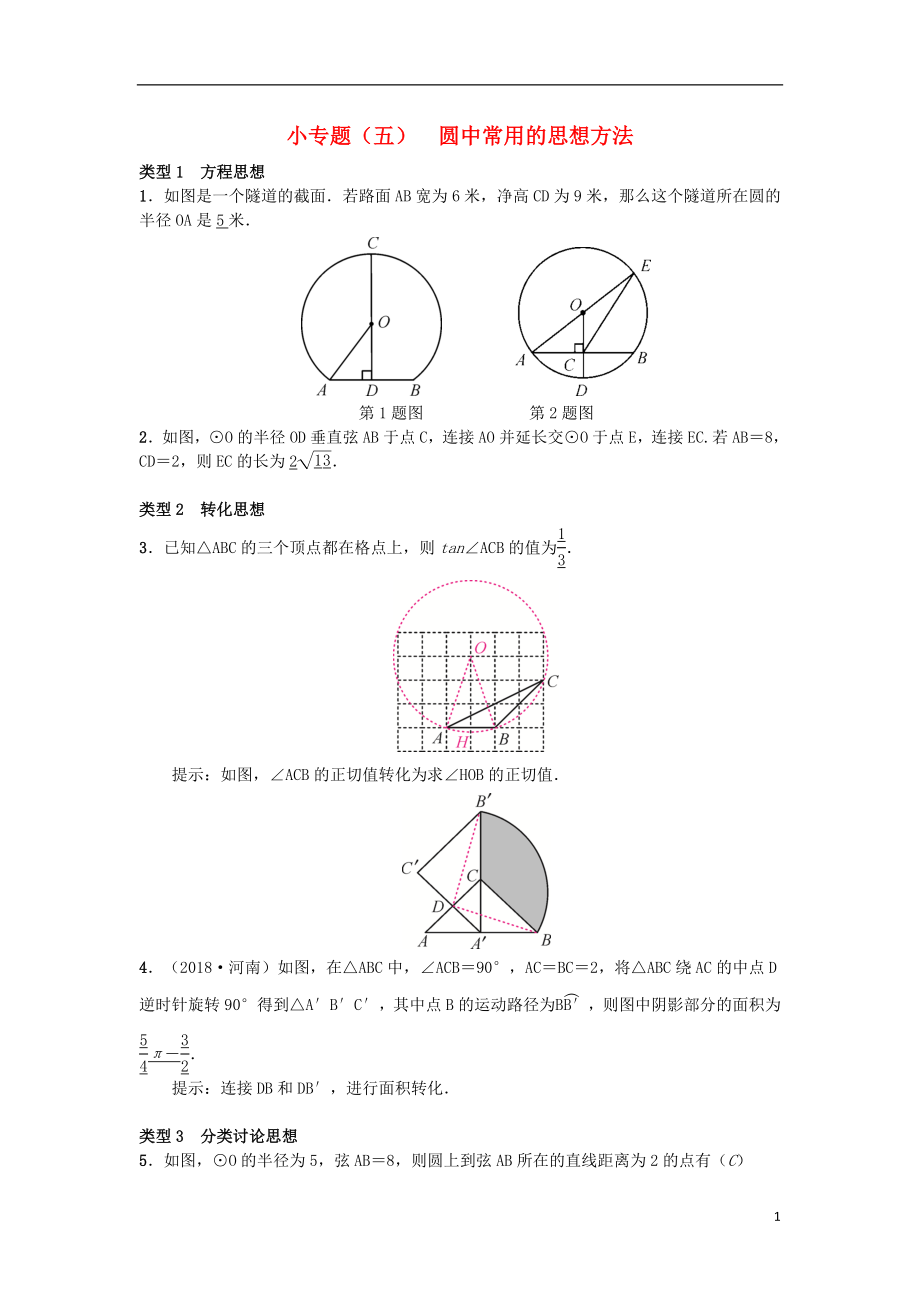
1．如圖是一個(gè)隧道的截面．若路面AB寬為6米，凈高CD為9米，那么這個(gè)隧道所在圓的半徑OA是5米．
第1題圖 第2題圖
2．如圖，⊙O的半徑OD垂直弦AB于點(diǎn)C，連接AO并延長(zhǎng)交⊙O于點(diǎn)E，連接EC.若AB＝8，CD＝2，則EC的長(zhǎng)為2．
類型2 轉(zhuǎn)化思想
3．已知△ABC的三個(gè)頂點(diǎn)都在格點(diǎn)上，則tan∠ACB的值為．
提示：如圖，∠ACB的正切值轉(zhuǎn)化為求∠HOB的正切值．
4．（2018·河南）如圖，在△ABC中，∠ACB＝90°，AC＝BC＝2，將△ABC繞AC的中點(diǎn)D
2、逆時(shí)針旋轉(zhuǎn)90°得到△A′B′C′，其中點(diǎn)B的運(yùn)動(dòng)路徑為，則圖中陰影部分的面積為π－．
提示：連接DB和DB′，進(jìn)行面積轉(zhuǎn)化．
類型3 分類討論思想
5．如圖，⊙O的半徑為5，弦AB＝8，則圓上到弦AB所在的直線距離為2的點(diǎn)有（C）
A．1個(gè) B．2個(gè)
C．3個(gè) D．0個(gè)
第5題圖 第6題圖
6．如圖，Rt△ABC的斜邊AB與量角器的直徑恰好重合，B點(diǎn)與0刻度線的一端重合，∠ABC＝40°，射線CD繞點(diǎn)C旋轉(zhuǎn)，與量角器外沿交于點(diǎn)D.若射線CD將△ABC分割出以BC為邊的等腰三角形，則點(diǎn)D在量角器上對(duì)應(yīng)的度數(shù)是80°或140°．
7．已知⊙O的直徑是10 cm，弦AB∥CD，AB＝6 cm，CD＝8 cm，則AB與CD之間的距離為7__cm或1__cm．
8．（2018·寧波）如圖，正方形ABCD的邊長(zhǎng)為8，M是AB的中點(diǎn)，P是BC邊上的動(dòng)點(diǎn)，連接PM，以點(diǎn)P為圓心，PM長(zhǎng)為半徑作⊙P.當(dāng)⊙P與正方形ABCD的邊相切時(shí)，BP的長(zhǎng)為3或4．
提示：圓分別與CD，AD相切．
類型4 整體思想
9．如圖，點(diǎn)A，B，C，D，E在⊙O上，且的度數(shù)為50°，則∠B＋∠D的度數(shù)為155°．
3
（安徽專版）2018年秋九年級(jí)數(shù)學(xué)下冊(cè) 小專題（五）圓中常用的思想方法習(xí)題 （新版）滬科版
