2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題3 數(shù)列學(xué)案

《2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題3 數(shù)列學(xué)案》由會(huì)員分享，可在線閱讀，更多相關(guān)《2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題3 數(shù)列學(xué)案（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

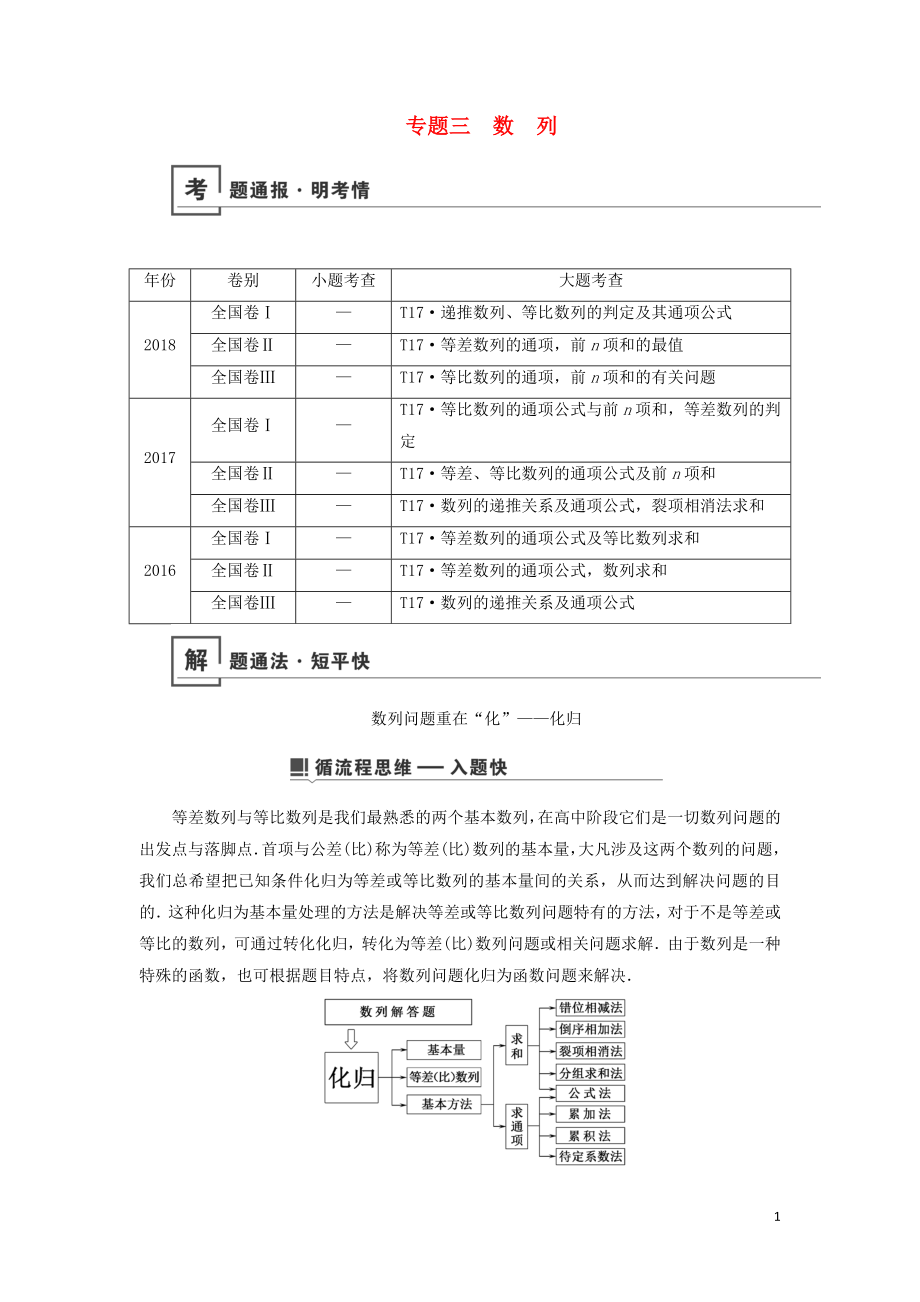
1、專題三　數(shù)　列 年份 卷別 小題考查 大題考查 2018 全國(guó)卷Ⅰ — T17·遞推數(shù)列、等比數(shù)列的判定及其通項(xiàng)公式 全國(guó)卷Ⅱ — T17·等差數(shù)列的通項(xiàng)，前n項(xiàng)和的最值 全國(guó)卷Ⅲ — T17·等比數(shù)列的通項(xiàng)，前n項(xiàng)和的有關(guān)問題 2017 全國(guó)卷Ⅰ — T17·等比數(shù)列的通項(xiàng)公式與前n項(xiàng)和，等差數(shù)列的判定 全國(guó)卷Ⅱ — T17·等差、等比數(shù)列的通項(xiàng)公式及前n項(xiàng)和 全國(guó)卷Ⅲ — T17·數(shù)列的遞推關(guān)系及通項(xiàng)公式，裂項(xiàng)相消法求和 2016 全國(guó)卷Ⅰ — T17·等差數(shù)列的通項(xiàng)公式及等比數(shù)列求和 全國(guó)卷Ⅱ — T17·等差數(shù)列的通

2、項(xiàng)公式，數(shù)列求和 全國(guó)卷Ⅲ — T17·數(shù)列的遞推關(guān)系及通項(xiàng)公式 數(shù)列問題重在“化”——化歸 等差數(shù)列與等比數(shù)列是我們最熟悉的兩個(gè)基本數(shù)列，在高中階段它們是一切數(shù)列問題的出發(fā)點(diǎn)與落腳點(diǎn)．首項(xiàng)與公差(比)稱為等差(比)數(shù)列的基本量，大凡涉及這兩個(gè)數(shù)列的問題，我們總希望把已知條件化歸為等差或等比數(shù)列的基本量間的關(guān)系，從而達(dá)到解決問題的目的．這種化歸為基本量處理的方法是解決等差或等比數(shù)列問題特有的方法，對(duì)于不是等差或等比的數(shù)列，可通過轉(zhuǎn)化化歸，轉(zhuǎn)化為等差(比)數(shù)列問題或相關(guān)問題求解．由于數(shù)列是一種特殊的函數(shù)，也可根據(jù)題目特點(diǎn)，將數(shù)列問題化歸為函數(shù)問題來解決． 【典例】　S

3、n為數(shù)列{an}的前n項(xiàng)和．已知an>0，a＋2an＝4Sn＋3． (1)求{an}的通項(xiàng)公式； (2)設(shè)bn＝，求數(shù)列{bn}的前n項(xiàng)和． [解題示范]　(1)由a＋2an＝4Sn＋3， ① 可知a＋2an＋1＝4Sn＋1＋3. ② ②－①，得a－a＋2(an＋1－an)＝4an＋1， 即2(an＋1＋an)＝a－a＝(an＋1＋an)(an＋1－an)． 由an>0，得an＋1－an＝2.? 又a＋2a1＝4a1＋3， 解得a1＝－1(舍去)或a1＝3.所以{an}是首項(xiàng)為3，公差為2的等差數(shù)列，通項(xiàng)公式為an＝2n＋1． (2)由an＝2n＋1可知 bn＝＝ ＝.? 設(shè)數(shù)列{bn}的前n項(xiàng)和為Tn，則 Tn＝b1＋b2＋…＋bn ＝ ＝． ?化歸：由條件化歸為等差數(shù)列項(xiàng)與項(xiàng)之間的關(guān)系． ?化歸：把數(shù)列的通項(xiàng)分拆后使得求和時(shí)某些項(xiàng)可以相消，即為裂項(xiàng)相消法求和． 對(duì)于數(shù)列的備考：一是準(zhǔn)確掌握數(shù)列中an與Sn之間的關(guān)系，這是解決數(shù)列問題的基礎(chǔ)；二是重視等差與等比數(shù)列的復(fù)習(xí)，熟悉其基本概念、公式和性質(zhì)，這是解決數(shù)列問題的根本；三是注意數(shù)列與函數(shù)、不等式等的綜合問題，掌握解決此類問題的通法；四是在知識(shí)的復(fù)習(xí)和解題過程中體會(huì)其中所蘊(yùn)含的數(shù)學(xué)思想方法，如分類討論、數(shù)形結(jié)合、等價(jià)轉(zhuǎn)化、函數(shù)與方程思想等． 3