《2022年高中數(shù)學(xué)(北師大版)選修1-2教案:第1章 一道回歸分析題的思維拓展與延伸》由會員分享���,可在線閱讀���,更多相關(guān)《2022年高中數(shù)學(xué)(北師大版)選修1-2教案:第1章 一道回歸分析題的思維拓展與延伸(4頁珍藏版)》請在裝配圖網(wǎng)上搜索。
1�、
2022年高中數(shù)學(xué)(北師大版)選修1-2教案:第1章 一道回歸分析題的思維拓展與延伸
一、回歸分析的基本步驟:
(1) 畫出兩個變量的散點圖.
(2) 求回歸直線方程.
(3) 用回歸直線方程進(jìn)行預(yù)報.
下面我們通過案例����,進(jìn)一步學(xué)習(xí)、拓展與延伸回歸分析的基本思想及其應(yīng)用.
二����、舉例:
例1. 從某大學(xué)中隨機選取 8 名女大學(xué)生,其身高和體重數(shù)據(jù)如表
編號
1
2
3
4
5
6
7
8
身高/cm
165
165
157
170
175
165
155
170
體重/kg
48
57
50
54
64
61
43
59
2���、
求根據(jù)女大學(xué)生的身高預(yù)報體重的回歸方程�����,并預(yù)報一名身高為 172 cm 的女大學(xué)生的體重.
解:由于問題中要求根據(jù)身高預(yù)報體重����,因此選取身高為自變量 x ,體重為因變量 y .
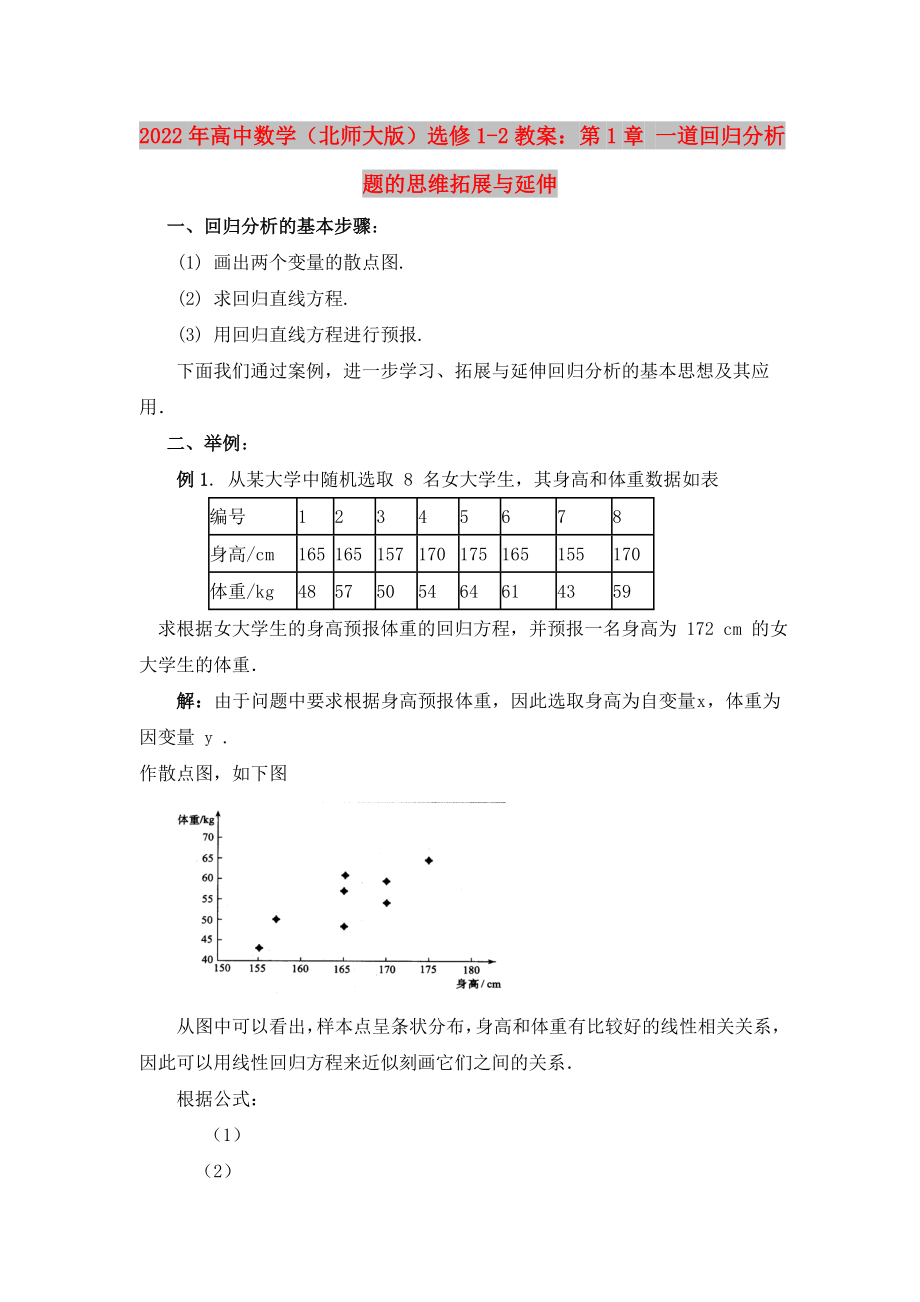
作散點圖�����,如下圖
從圖中可以看出���,樣本點呈條狀分布,身高和體重有比較好的線性相關(guān)關(guān)系��,因此可以用線性回歸方程來近似刻畫它們之間的關(guān)系.
根據(jù)公式:
(1)
(2)
其中��,()成為樣本點的中心.
可以得到.
于是得到回歸方程.
因此���,對于身高172 cm 的女大學(xué)生��,由回歸方程可以預(yù)報其體重為
( kg ) .
是斜率的估計值�����,說明身高 x 每增加1個單位時���,體重y就
3�����、增加0.849 位�����,這表明體重與身高具有正的線性相關(guān)關(guān)系.
三.思維拓展與延伸
1.如何描述它們之間線性相關(guān)關(guān)系的強弱���?
在必修 3 中,我們介紹了用相關(guān)系數(shù)����;來衡量兩個變量之間線性相關(guān)關(guān)系的方法.本相關(guān)系數(shù)的具體計算公式為.
當(dāng)r>0時,表明兩個變量正相關(guān)�����;當(dāng)r<0時����,表明兩個變量負(fù)相關(guān).r的絕對值越接近1���,表明兩個變量的線性相關(guān)性越強;r的絕對值接近于0時��,表明兩個變量之間幾乎不存在線性相關(guān)關(guān)系.通常�����,當(dāng)r的絕對值大于0. 75 時認(rèn)為兩個變量有很強的線性相關(guān)關(guān)系.
在本例中���,可以計算出r =0. 798.這表明體重與身高有很強的線性相關(guān)關(guān)系,從而也表明我們建立的回歸模型是有意義
4�����、的.
2.如何理解與間的誤差
顯然���,身高172cm 的女大學(xué)生的體重不一定是60. 316 kg��,但一般可以認(rèn)為她的體重接近于60 . 316 kg .如下圖中的樣本點和回歸直線的相互位置說明了這一點.
由于所有的樣本點不共線�����,而只是散布在某一條直線的附近�����,所以身高和體重的關(guān)系可用下面的線性回歸模型來表示:
這里a和b為模型的未知參數(shù)����,e是y與之間的誤差.通常e為隨機變量,稱為隨機誤差�����,它的均值 E(e)=0�,方差D(e)=>0 .這樣線性回歸模型的完整表達(dá)式為: (3)
在線性回歸模型(3)中,隨機誤差e的方差護(hù)越小��,通過回歸直線
預(yù)報真實值y的精度越高.隨機
5���、誤差是引起預(yù)報值與真實值 y 之間的誤差的原因之一����,大小取決于隨機誤差的方差.
另一方面�����,由于公式(1)和(2)中 和為截距和斜率的估計值,它們與真實值a和b之間也存在誤差�,這種誤差是引起預(yù)報值與真實值y之間誤差的另一個原因.
3. 產(chǎn)生隨機誤差項e的原因是什么?
一個人的體重值除了受身高的影響外,還受許多其他因素的影響.例如飲食習(xí)慣�、是否喜歡運動、度量誤差等.事實上����,我們無法知道身高和體重之間的確切關(guān)系是什么,這里只是利用線性回歸方程來近似這種關(guān)系.這種近似以及上面提到的影響因素都是產(chǎn)生隨機誤差 e的原因.
因為隨機誤差是隨機變量��,所以可以通過這個隨機變量的數(shù)字特征來刻畫它的一些總體
6�����、特征.均值是反映隨機變量取值平均水平的數(shù)字特征�,方差是反映隨機變量集中于均值程度的數(shù)字特征,而隨機誤差的均值為0����,因此可以用方差來衡量隨機誤差的大?。?
4. 用身高預(yù)報體重時,需要注意哪些問題�?
需要注意下列問題:
(1).回歸方程只適用于我們所研究的樣本的總體.例如,不能用女大學(xué)生的身高和體重之間的回歸方程���,描述女運動員的身高和體重之間的關(guān)系.同樣��,不能用生長在南方多雨地區(qū)的樹木的高與直徑之間的回歸方程�����,描述北方干旱地區(qū)的樹木的高與直徑之間的關(guān)系.
(2).我們所建立的回歸方程一般都有時間性.例如��,不能用 20 世紀(jì) 80 年代的身高體重數(shù)據(jù)所建立的回歸方程�,描述現(xiàn)在的身高和體重之間的關(guān)系.
(3).樣本取值的范圍會影響回歸方程的適用范圍.例如,我們的回歸方程是由女大學(xué)生身高和體重數(shù)據(jù)建立的����,那么用它來描述一個人幼兒時期的身高和體重之間的關(guān)系就不恰當(dāng)(即在回歸方程中,解釋變量 x 的樣本的取值范圍為[155cm,170cm〕 �,而用這個方程計算 x-70cm 時的y值,顯然不合適.)
(4).不能期望回歸方程得到的預(yù)報值就是預(yù)報變量的精確值.事實上����,它是預(yù)報變量的可能取值的平均值.
 2022年高中數(shù)學(xué)(北師大版)選修1-2教案:第1章 一道回歸分析題的思維拓展與延伸
2022年高中數(shù)學(xué)(北師大版)選修1-2教案:第1章 一道回歸分析題的思維拓展與延伸