《陜西省澄城縣寺前中學(xué)高中數(shù)學(xué) 簡(jiǎn)單幾何體的體積學(xué)案(通用)》由會(huì)員分享,可在線閱讀�,更多相關(guān)《陜西省澄城縣寺前中學(xué)高中數(shù)學(xué) 簡(jiǎn)單幾何體的體積學(xué)案(通用)(3頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1�����、陜西省澄城縣寺前中學(xué)高一數(shù)學(xué) 簡(jiǎn)單幾何體的體積 學(xué)案
學(xué)習(xí)目標(biāo)
1.在上一節(jié)學(xué)習(xí)的基礎(chǔ)上����,會(huì)用公式求柱、錐���、臺(tái)體的體積.了解柱�、錐��、臺(tái)體的體積之間的關(guān)系.
2.記住球的表面積和體積公式,并進(jìn)行有關(guān)計(jì)算.
學(xué)習(xí)重點(diǎn)
柱體����、錐體、臺(tái)體的體積的計(jì)算.會(huì)用公式求球的表面積和體積.
學(xué)習(xí)難點(diǎn)
與球有關(guān)的組合體的體積計(jì)算.
閱讀課本P45---P48,認(rèn)真完成學(xué)案:
1.柱���、錐�����、臺(tái)體的體積
V柱體=Sh(S為柱體的底面積����,h為柱體的高).
V錐體=Sh(S為錐體的底面積��,h為錐體的高).
V臺(tái)體=(S上+S下+)h(S上�����,S下分別為棱臺(tái)的上���,下底面積,h為高).
預(yù)習(xí)交流1
2����、
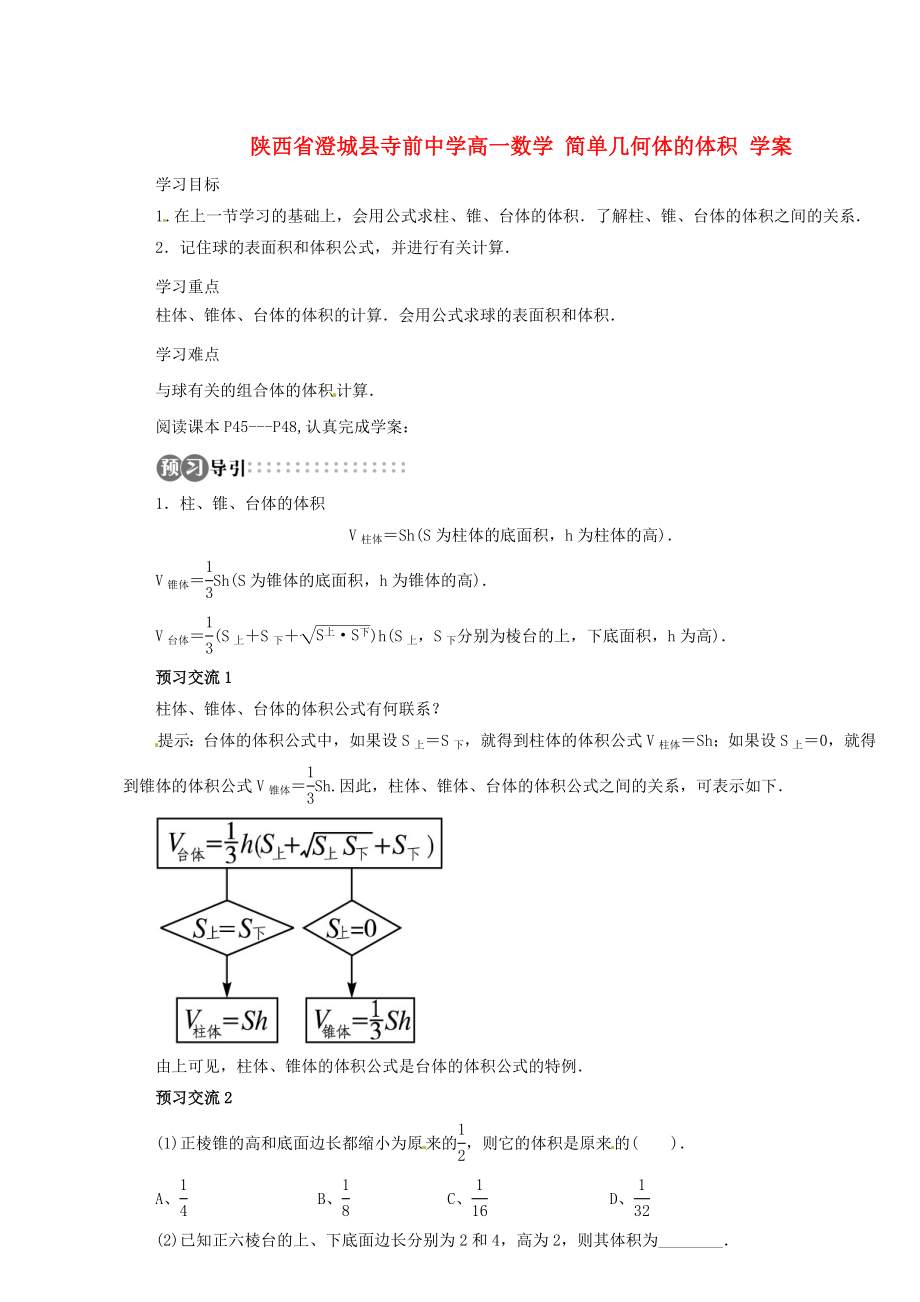
柱體��、錐體�、臺(tái)體的體積公式有何聯(lián)系���?
提示:臺(tái)體的體積公式中���,如果設(shè)S上=S下,就得到柱體的體積公式V柱體=Sh�;如果設(shè)S上=0,就得到錐體的體積公式V錐體=Sh.因此���,柱體��、錐體��、臺(tái)體的體積公式之間的關(guān)系����,可表示如下.
由上可見(jiàn)�,柱體、錐體的體積公式是臺(tái)體的體積公式的特例.
預(yù)習(xí)交流2
(1)正棱錐的高和底面邊長(zhǎng)都縮小為原來(lái)的�,則它的體積是原來(lái)的( ).
A����、 B�����、 C�����、 D�、
(2)已知正六棱臺(tái)的上、下底面邊長(zhǎng)分別為2和4�,高為2,則其體積為_(kāi)_______.
2.球的表面積和體積
S球面=4πR2���,V球=πR3(其中R為球的半徑).
3���、預(yù)習(xí)交流3
(1)若球的半徑由R增加為2R,則這個(gè)球的表面積變?yōu)樵瓉?lái)的________倍�,體積變?yōu)樵瓉?lái)的________倍.
(2)若一個(gè)球的體積為4π,則它的表面積為_(kāi)_____.
合作探究 1 : 課本 P46 例4 ���, P47 例6���,例7
合作探究2 :
1、如圖所示�,一個(gè)空間幾何體的主視圖、左視圖��、俯視圖為全等的等腰直角三角形����,如果直角三角形的直角邊長(zhǎng)為1,那么這個(gè)幾何體的體積為( )
A���、1 B�����、 C����、 D��、
2.如圖是某幾何體的三視圖��,則該幾何體的體積為( ).
A.π+12
B.π+18
C.9π+42
D.36π+18
當(dāng)堂檢測(cè):
1. 已知高為3的直三棱柱ABC-A′B′C′的底面是邊長(zhǎng)為1的正三角形����,則三棱錐B′-ABC的體積為( ).
A�����、
B���、
C、
D��、
2.已知兩個(gè)球的半徑之比為1∶2����,則這兩個(gè)球的表面積之比為( ).
A.1∶2 B.1∶4 C.1∶6 D.1∶8
3.圓臺(tái)的上、下底面的面積分別為π�,4π,側(cè)面積是6π��,這個(gè)圓臺(tái)的體積是( ).
A��、 B���、2π C���、 D�、
 陜西省澄城縣寺前中學(xué)高中數(shù)學(xué) 簡(jiǎn)單幾何體的體積學(xué)案(通用)
陜西省澄城縣寺前中學(xué)高中數(shù)學(xué) 簡(jiǎn)單幾何體的體積學(xué)案(通用)