《2020屆高考數(shù)學(xué) 考前30天解答題復(fù)習(xí)預(yù)測(cè)試題1》由會(huì)員分享,可在線閱讀�����,更多相關(guān)《2020屆高考數(shù)學(xué) 考前30天解答題復(fù)習(xí)預(yù)測(cè)試題1(3頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索����。
1、高考預(yù)測(cè)試題(1)·解答題1
適用:新課標(biāo)地區(qū)
1. (本題滿分14分)
某初級(jí)中學(xué)共有學(xué)生2000名�,各年級(jí)男、女生人數(shù)如下表:
初一年級(jí)
初二年級(jí)
初三年級(jí)
女生
373
x
y
男生
377
370
z
已知在全校學(xué)生中隨機(jī)抽取1名�,抽到初二年級(jí)女生的概率是0.19.
(1) 現(xiàn)用分層抽樣的方法在全校抽取48名學(xué)生,問應(yīng)在初三年級(jí)抽取多少名����?
(2) 已知y245,z245,求初三年級(jí)中女生比男生多的概率.
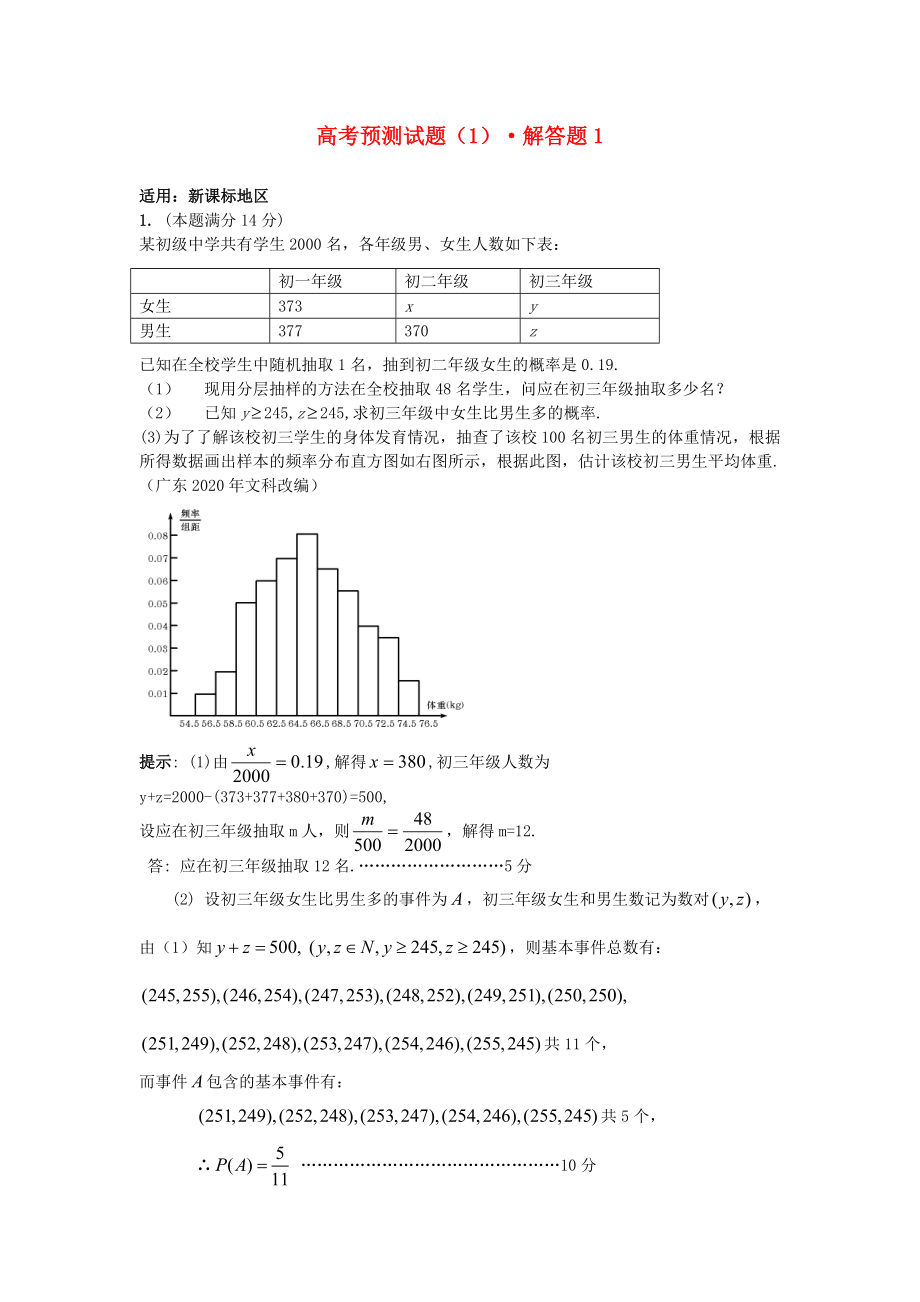
(3)為了了解該校初三學(xué)生的身體發(fā)育情況,抽查了該校100名初三男生的體重情況���,根據(jù)所得數(shù)據(jù)畫出樣本的頻率分布直方圖如右圖
2��、所示�,根據(jù)此圖����,估計(jì)該校初三男生平均體重. (廣東2020年文科改編)
提示: (1)由,解得,初三年級(jí)人數(shù)為
y+z=2000-(373+377+380+370)=500,
設(shè)應(yīng)在初三年級(jí)抽取m人�����,則,解得m=12.
答: 應(yīng)在初三年級(jí)抽取12名.………………………5分
(2) 設(shè)初三年級(jí)女生比男生多的事件為���,初三年級(jí)女生和男生數(shù)記為數(shù)對(duì)�,
由(1)知���,則基本事件總數(shù)有:
共11個(gè)����,
而事件包含的基本事件有:
共5個(gè)��,
∴ …………………………………………10分
(3)由圖可知:100男生在各組的頻率分別為:0.02,0.04,0.1,0.
3�、12,0.14,0.16,
0.13,0.11,0.08,0.07,0.03;各組的組中值分別為:55.5,57.5,59.5,61.5,63.5,65.5,67.5,
69.5,71.5,73.5,75.5;所以平均體重為
………………………………………………………………………14分
點(diǎn)評(píng):該題考查分層抽樣與古典概型以及頻率分布直方圖和利用組中值估計(jì)平均數(shù),還考查了直線上滿足一定條件的整點(diǎn)個(gè)數(shù)��。是課本上擲骰子例題的變形�。是容易題.
2. (本小題滿分14分) 如圖,四棱錐P—ABCD中��,底面ABCD是矩形,PA⊥底面ABCD����,PA=AB=1,AD=��,點(diǎn)F是PB的中點(diǎn)��,點(diǎn)E在邊BC上
4���、移動(dòng).
(1)求三棱錐E-PAD的體積����;
(2)點(diǎn)E為BC的中點(diǎn)時(shí)��,試判斷EF與平面PAC的位置關(guān)系���,并說明理由�����;
(3)證明:無論點(diǎn)E在BC邊的何處�����,都有PE⊥AF.
提示:(1)∵PA⊥底面ABCD�,∴PA⊥AD,
∴三棱錐E-PAD的體積為.…………4分
(2)當(dāng)點(diǎn)E為BC的中點(diǎn)時(shí)�����,
EF與平面PAC平行.∵在△PBC中����,
E����、F分別為BC、PB的中點(diǎn)���,
∴EF//PC 又EF平面PAC�����,
而PC平面PAC ∴EF//平面PAC.…………………………9分
(3)∵PA⊥平面ABCD�����,BE平面ABCD����,
∴EB⊥PA.又EB⊥AB,AB∩AP=
5��、A����,AB,AP平面PAB�,
∴EB⊥平面PAB,
又AF平面PAB����,∴AF⊥BE.
又PA=AB=1,點(diǎn)F是PB的中點(diǎn)�����,∴AF⊥PB���,
又∵PB∩BE=B���,PB,BE平面PBE�,∴AF⊥平面PBE.
∵PE平面PBE����,∴AF⊥PE.………………………………………14分
點(diǎn)評(píng):該題考查棱錐的體積計(jì)算�、線面平行判定、線面垂直性質(zhì)��、判定����、線線垂直判定以及空間想象能力;是容易題.
3.(本小題滿分14分)
在中,A為銳角,角所對(duì)應(yīng)的邊分別為��,且
(I)求的值����;
(II)若��,求的值����。(2020四川卷理改編)
提示:(Ⅰ)為銳角,又����,
�����,�����,
∵�����,
…………………………………………8分
(Ⅱ)由(Ⅰ)知,.
由正弦定理得
���,即,
��,
�,
……………………………………14分
點(diǎn)評(píng):本小題主要考查同角三角函數(shù)間的關(guān)系,兩角和差的三角函數(shù)�、二倍角公式、正弦定理等基礎(chǔ)知識(shí)及基本運(yùn)算能力�����。
 2020屆高考數(shù)學(xué) 考前30天解答題復(fù)習(xí)預(yù)測(cè)試題1
2020屆高考數(shù)學(xué) 考前30天解答題復(fù)習(xí)預(yù)測(cè)試題1