《高中數(shù)學(xué)《函數(shù)y=Asin(ωx+φ)》同步練習(xí)8 新人教A版必修4》由會員分享��,可在線閱讀�,更多相關(guān)《高中數(shù)學(xué)《函數(shù)y=Asin(ωx+φ)》同步練習(xí)8 新人教A版必修4(3頁珍藏版)》請在裝配圖網(wǎng)上搜索���。
1�、高中數(shù)學(xué)《函數(shù)y=Asin(ωx+φ)》同步練習(xí)8 新人教A版必修4
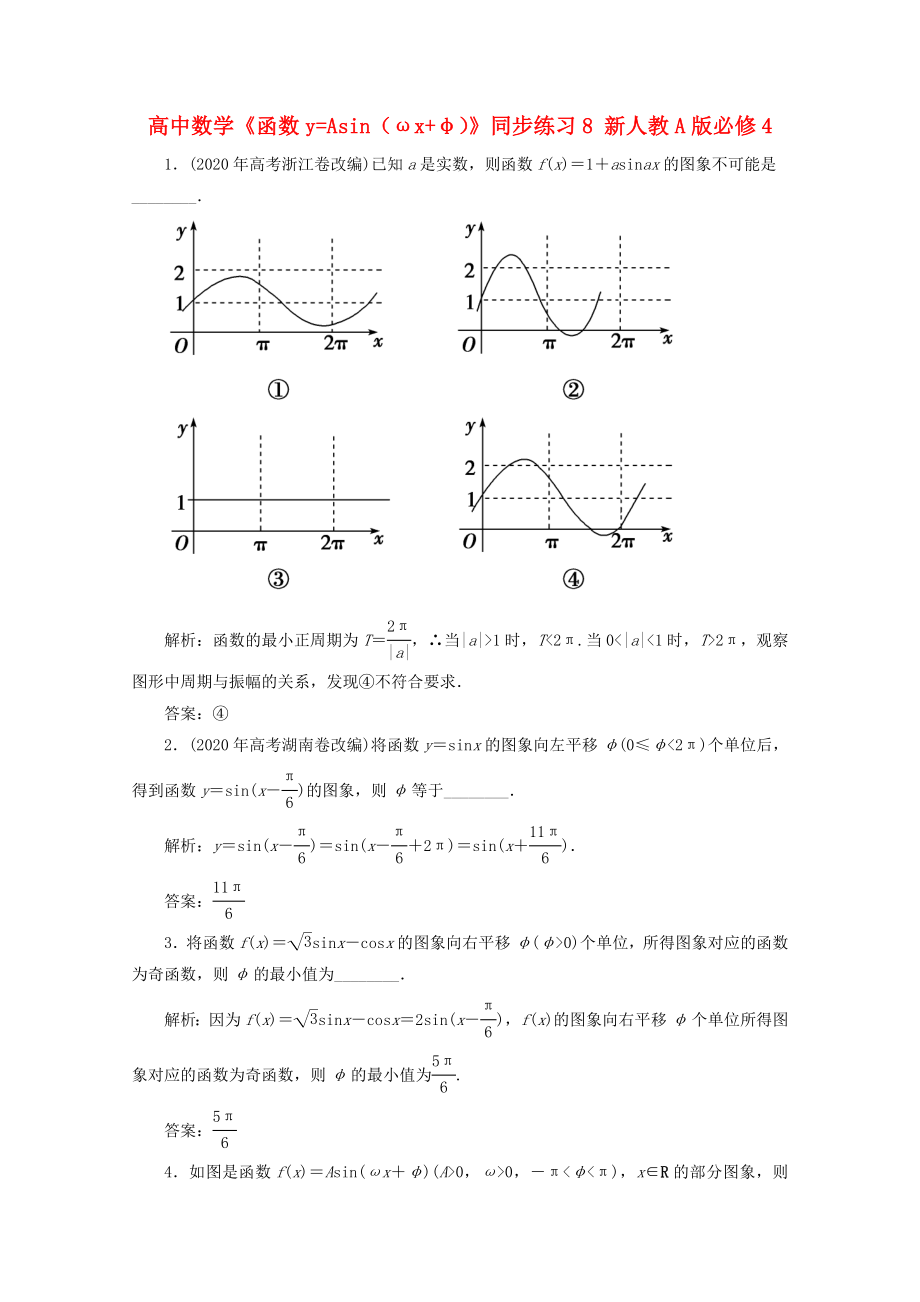
1.(2020年高考浙江卷改編)已知a是實數(shù)���,則函數(shù)f(x)=1+asinax的圖象不可能是________.
解析:函數(shù)的最小正周期為T=�,∴當(dāng)|a|>1時,T<2π.當(dāng)0<|a|<1時�����,T>2π�����,觀察圖形中周期與振幅的關(guān)系����,發(fā)現(xiàn)④不符合要求.
答案:④
2.(2020年高考湖南卷改編)將函數(shù)y=sinx的圖象向左平移φ(0≤φ<2π)個單位后,得到函數(shù)y=sin(x-)的圖象����,則φ等于________.
解析:y=sin(x-)=sin(x-+2π)=sin(x+).
答案:
3.將函數(shù)f(x)=sin
2��、x-cosx的圖象向右平移φ(φ>0)個單位�����,所得圖象對應(yīng)的函數(shù)為奇函數(shù)���,則φ的最小值為________.
解析:因為f(x)=sinx-cosx=2sin(x-)����,f(x)的圖象向右平移φ個單位所得圖象對應(yīng)的函數(shù)為奇函數(shù),則φ的最小值為.
答案:
4.如圖是函數(shù)f(x)=Asin(ωx+φ)(A>0����,ω>0,-π<φ<π)�,x∈R的部分圖象,則下列命題中�����,正確命題的序號為________.
①函數(shù)f(x)的最小正周期為;
②函數(shù)f(x)的振幅為2��;
③函數(shù)f(x)的一條對稱軸方程為x=π�����;
④函數(shù)f(x)的單調(diào)遞增區(qū)間為[����,π]����;
⑤函數(shù)的解析式為f(x)=sin(2x-π)
3����、.
解析:據(jù)圖象可得:A=���,=-?T=π���,故ω=2,又由f()=?sin(2×+φ)=1�,解得φ=2kπ-(k∈Z),又-π<φ<π��,故φ=-��,故f(x)=sin(2x-)��,依次判斷各選項��,易知①②是錯誤的����,由圖象易知x=是函數(shù)圖象的一條對稱軸���,故③正確�,④函數(shù)的單調(diào)遞增區(qū)間有無窮多個,區(qū)間[����,]只是函數(shù)的一個單調(diào)遞增區(qū)間,⑤由上述推導(dǎo)易知正確.
答案:③⑤
5.(原創(chuàng)題)已知函數(shù)f(x)=sinωx+cosωx����,如果存在實數(shù)x1,使得對任意的實數(shù)x����,都有f(x1)≤f(x)≤f(x1+2020)成立,則ω的最小值為________.
解析:顯然結(jié)論成立只需保證區(qū)間[x1�,x1+202
4、0]能夠包含函數(shù)的至少一個完整的單調(diào)區(qū)間即可�����,且f(x)=sinωx+cosωx=sin(ωx+)��,則2020≥?ω≥.
答案:
6.(2020年蘇北四市質(zhì)檢)已知函數(shù)f(x)=sin2ωx+sinωx·sin(ωx+)+2cos2ωx����,x∈R(ω>0),在y軸右側(cè)的第一個最高點的橫坐標(biāo)為.
(1)求ω��;
(2)若將函數(shù)f(x)的圖象向右平移個單位后,再將得到的圖象上各點橫坐標(biāo)伸長到原來的4倍����,縱坐標(biāo)不變,得到函數(shù)y=g(x)的圖象�,求函數(shù)g(x)的最大值及單調(diào)遞減區(qū)間.
解:(1)f(x)=sin2ωx+cos2ωx+
=sin(2ωx+)+,
令2ωx+=���,將x=代入可得:ω=1.
(2)由(1)得f(x)=sin(2x+)+����,
經(jīng)過題設(shè)的變化得到的函數(shù)g(x)=sin(x-)+����,
當(dāng)x=4kπ+π,k∈Z時��,函數(shù)取得最大值.
令2kπ+≤x-≤2kπ+π(k∈Z)���,
∴4kπ+≤x≤4kπ+π(k∈Z).
即x∈[4kπ+�����,4kπ+π]����,k∈Z為函數(shù)的單調(diào)遞減區(qū)間.
高考學(xué)習(xí)網(wǎng)()
來源:高考學(xué)習(xí)網(wǎng)
 高中數(shù)學(xué)《函數(shù)y=Asin(ωx+φ)》同步練習(xí)8 新人教A版必修4
高中數(shù)學(xué)《函數(shù)y=Asin(ωx+φ)》同步練習(xí)8 新人教A版必修4