《（浙江專用）2020版高考數(shù)學(xué)一輪總復(fù)習(xí) 專題9 直線和圓的方程 9.1 直線方程和兩直線間的位置關(guān)系檢測(cè)》由會(huì)員分享，可在線閱讀，更多相關(guān)《（浙江專用）2020版高考數(shù)學(xué)一輪總復(fù)習(xí) 專題9 直線和圓的方程 9.1 直線方程和兩直線間的位置關(guān)系檢測(cè)（6頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1、9.1 直線方程和兩直線間的位置關(guān)系
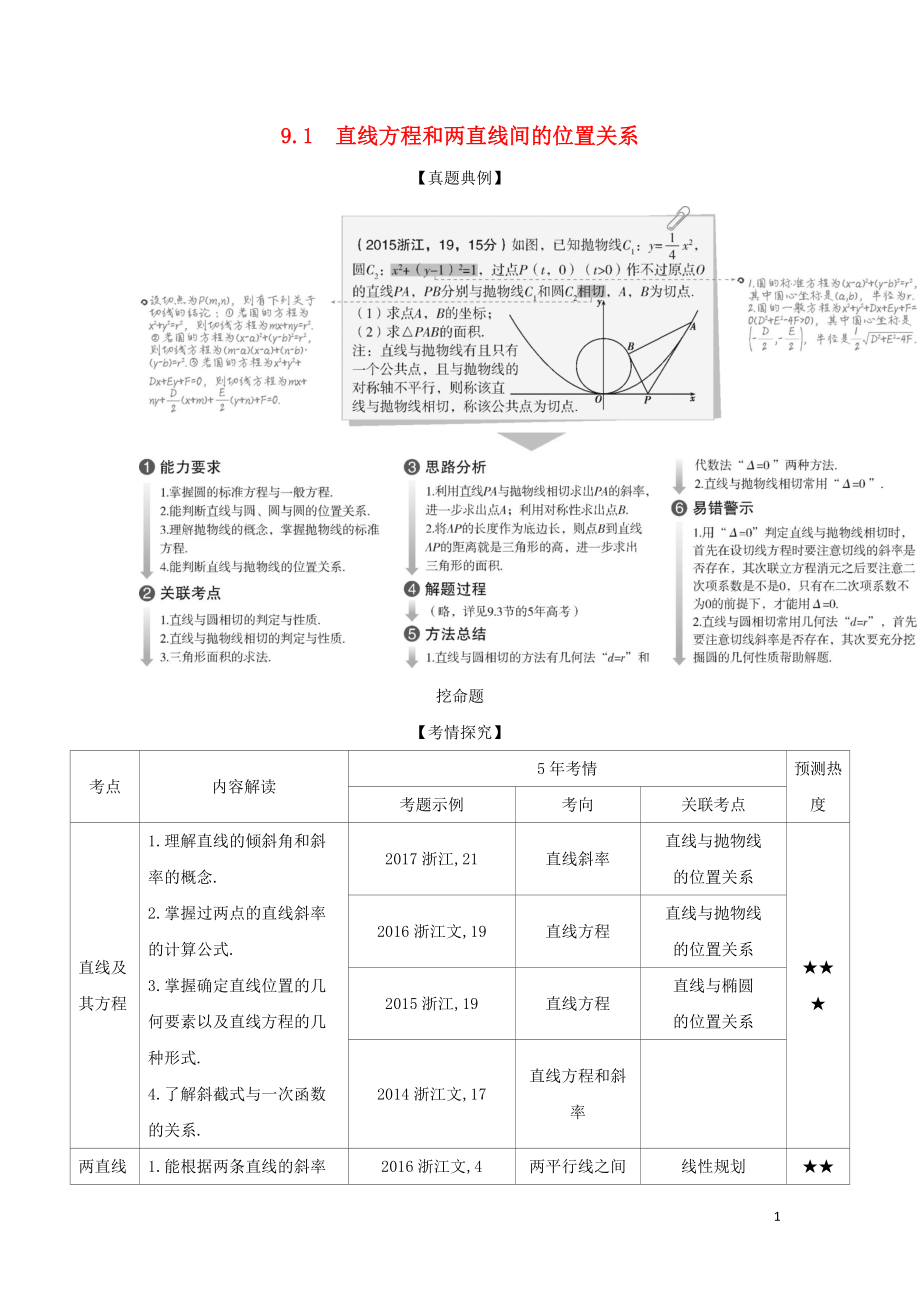
【真題典例】
挖命題
【考情探究】
考點(diǎn)
內(nèi)容解讀
5年考情
預(yù)測(cè)熱度
考題示例
考向
關(guān)聯(lián)考點(diǎn)
直線及其方程
1.理解直線的傾斜角和斜率的概念.
2.掌握過兩點(diǎn)的直線斜率的計(jì)算公式.
3.掌握確定直線位置的幾何要素以及直線方程的幾種形式.
4.了解斜截式與一次函數(shù)的關(guān)系.
2017浙江,21
直線斜率
直線與拋物線
的位置關(guān)系
★★★
2016浙江文,19
直線方程
直線與拋物線
的位置關(guān)系
2015浙江,19
直線方程
直線與橢圓
的位置關(guān)系
2014浙江文,17
直線方程和斜率
兩
2、直線間的位置關(guān)系
1.能根據(jù)兩條直線的斜率判定這兩條直線平行或垂直.
2.會(huì)求兩條直線的交點(diǎn)坐標(biāo).
3.掌握兩點(diǎn)間的距離公式、點(diǎn)到直線的距離公式,會(huì)求兩條平行直線間的距離.
2016浙江文,4
兩平行線之間的距離
線性規(guī)劃
★★★
分析解讀 1.考查基本概念、直線的傾斜角和斜率、兩直線的位置關(guān)系的判斷、點(diǎn)到直線的距離等,一般以選擇題、填空題的形式呈現(xiàn),此類題大都屬于中、低檔題.
2.求直線方程有時(shí)與其他曲線綜合進(jìn)行考查,以解答題形式出現(xiàn),此類題屬于難題.
3.求不同條件下的直線方程,主要方法是待定系數(shù)法,在使用待定系數(shù)法求直線方程時(shí),要注意形式的選擇,注意分斜率存在與不存
3、在進(jìn)行討論.
4.預(yù)計(jì)2020年高考中,仍將以直線的傾斜角與斜率、直線方程、兩直線的位置關(guān)系為命題的熱點(diǎn).
破考點(diǎn)
【考點(diǎn)集訓(xùn)】
考點(diǎn)一 直線及其方程
1.(2018浙江高考模擬卷,7) 已知P1(a1,b1)與P2(a2,b2)是直線y=kx+1(k為常數(shù))上兩個(gè)不同的點(diǎn),則關(guān)于x和y的方程組的解的情況是 ( )
A.無論k,P1,P2如何,總是無解
B.無論k,P1,P2如何,總有唯一解
C.存在k,P1,P2,使之恰有兩解
D.存在k,P1,P2,使之有無窮多解
答案 B
2.(2018浙江杭州地區(qū)重點(diǎn)中學(xué)第一學(xué)期期中,
4、9)已知a,b為正實(shí)數(shù),若直線y=x-a與曲線y=ln (x+b)相切,則的取值范圍為( )
A. B.(0,1) C.(0,+∞) D.[1,+∞)
答案 A
考點(diǎn)二 兩直線間的位置關(guān)系
1.(2017浙江杭州二模(4月),4)設(shè)k1,k2分別是直線l1,l2的斜率,則“l(fā)1∥l2”是“k1=k2”的( )
A.充分不必要條件
B.必要不充分條件
C.充分必要條件
D.既不充分也不必要條件
答案 A
2.(2017浙江鎮(zhèn)海中學(xué)模擬卷(一),8)已知直線l:Ax+By+C-1=0(A>0,B>0)過定點(diǎn)(m,0),若點(diǎn)(2,2)到直線l的最大距離為2,則+的最小
5、值為( )
A. B. C.4 D.
答案 C
煉技法
【方法集訓(xùn)】
方法 直線方程的求法
1.已知直線l:(2m+1)x+(m-2)y-5m=0.
(1)求證:直線l必經(jīng)過定點(diǎn);
(2)若直線l在兩坐標(biāo)軸上的截距相等,求直線l的方程.
解析 (1)證明:由題意得,m(2x+y-5)+(x-2y)=0,
由得
所以直線l必經(jīng)過定點(diǎn)(2,1).
(2)解法一:令x=0,得y=;令y=0,得x=.
由題意得=,解得m=0或-3,
則直線l的方程為x-2y=0或x+y-3=0.
解法二:因?yàn)橹本€l在兩坐標(biāo)軸上的截距相等,則直線l過原點(diǎn)或斜率為-1.
從而有m=0
6、或-=-1(m≠0且m≠2),
所以m=0或m=-3,
則直線l的方程為x-2y=0或x+y-3=0.
2.過點(diǎn)P(2,1)作直線l,與x軸正半軸,y軸正半軸分別交于A,B兩點(diǎn),求:
(1)△AOB面積的最小值及此時(shí)直線l的方程;
(2)直線l在兩坐標(biāo)軸上截距之和的最小值及此時(shí)直線l的方程;
(3)|AP|∶|PB|=3∶5時(shí),直線l的方程.
解析 設(shè)直線l:y-1=k(x-2),k<0,則A,B兩點(diǎn)的坐標(biāo)分別為,(0,1-2k).
(1)△AOB的面積S=(1-2k)=2+≥4,
當(dāng)且僅當(dāng)k=-時(shí),△AOB的面積取得最小值,為4,此時(shí)直線l的方程為x+2y-4=0.
(2
7、)解法一:直線l在兩坐標(biāo)軸上截距之和u=2-+1-2k=3+2(-k)+≥3+2,當(dāng)且僅當(dāng)k=-時(shí),直線l在兩坐標(biāo)軸上截距之和取得最小值,為3+2,此時(shí)直線l的方程為x+y-2-=0.
解法二:設(shè)直線l的方程為+=1(a>0,b>0),由l過點(diǎn)P(2,1)得+=1,直線l在兩坐標(biāo)軸上截距之和μ=a+b=(a+b)=3++≥3+2,當(dāng)且僅當(dāng)即時(shí),μ取得最小值,為3+2,此時(shí)直線l的方程為x+y-2-=0.
(3)當(dāng)|AP|∶|PB|=3∶5時(shí),5=3,可得k=-,此時(shí)直線l的方程為5x+6y-16=0.
過專題
【五年高考】
統(tǒng)一命題、省(區(qū)、市)卷題組
考點(diǎn) 兩直線間的位置關(guān)系
8、1.(2018北京理,7,5分)在平面直角坐標(biāo)系中,記d為點(diǎn)P(cos θ,sin θ)到直線x-my-2=0的距離.當(dāng)θ,m變化時(shí),d的最大值為 ( )
A.1 B.2 C.3 D.4
答案 C
2.(2016四川, 9,5分)設(shè)直線l1,l2分別是函數(shù)f(x)=圖象上點(diǎn)P1,P2處的切線,l1與l2垂直相交于點(diǎn)P,且l1,l2分別與y軸相交于點(diǎn)A,B,則△PAB的面積的取值范圍是( )
A.(0,1) B.(0,2) C.(0,+∞) D.(1,+∞)
答案 A
【三年模擬】
一、選擇題(每小題4分,共12分)
1.(201
9、9屆浙江高考模擬試卷(二),4)已知A(-2,a),B(3,b),直線AB的斜率為,則|AB|=( )
A.5 B.5 C.10 D.10
答案 D
2.(2018浙江9+1高中聯(lián)盟期中,3)“m=2”是“直線2x+(m+1)y+4=0與直線mx+3y-2=0平行”的( )
A.充分不必要條件
B.必要不充分條件
C.充分必要條件
D.既不充分也不必要條件
答案 A
3.(2018浙江鎮(zhèn)海中學(xué)階段性測(cè)試,3)若直線2(a+1)x+ay-2=0與直線ax+2y+1=0垂直,則a=( )
10、
A.-2 B.0 C.0或-2 D.2±2
答案 C
二、填空題(單空題4分,多空題6分,共20分)
4.(2019屆浙江“七彩陽(yáng)光”聯(lián)盟期初聯(lián)考,17)已知直線l與橢圓C:+y2=1交于A、B兩點(diǎn),l與x軸、y軸分別交于C、D兩點(diǎn).若C、D是線段AB的兩個(gè)三等分點(diǎn),則直線l的斜率為 .?
答案 ±
5.(2018浙江高考模擬卷,11)已知直線l1:ax+y+2=0,l2:(a2-3)x+2y+1=0,若a∈R,則直線l1過定點(diǎn) ;若l1∥l2,則實(shí)數(shù)a= .?
答案 (0,-2);3或-1
6.(2017浙江金華十校調(diào)研,11)已知直線l1:2x-2y+1=0,直線l2:x+by-3=0,若l1⊥l2,則b= ;若l1∥l2,則兩直線間的距離是 .?
答案 1;
7.(2018浙江鎮(zhèn)海中學(xué)階段性測(cè)試,15)直線l1與直線l2交于一點(diǎn)P,且l1的斜率為,l2的斜率為2k,直線l1、l2與x軸圍成一個(gè)等腰三角形,則正實(shí)數(shù)k的所有可能取值為 .?
答案 或
6
（浙江專用）2020版高考數(shù)學(xué)一輪總復(fù)習(xí) 專題9 直線和圓的方程 9.1 直線方程和兩直線間的位置關(guān)系檢測(cè)
