【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第2篇 二次函數(shù)學(xué)案 理

《【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第2篇 二次函數(shù)學(xué)案 理》由會(huì)員分享，可在線閱讀，更多相關(guān)《【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第2篇 二次函數(shù)學(xué)案 理（6頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

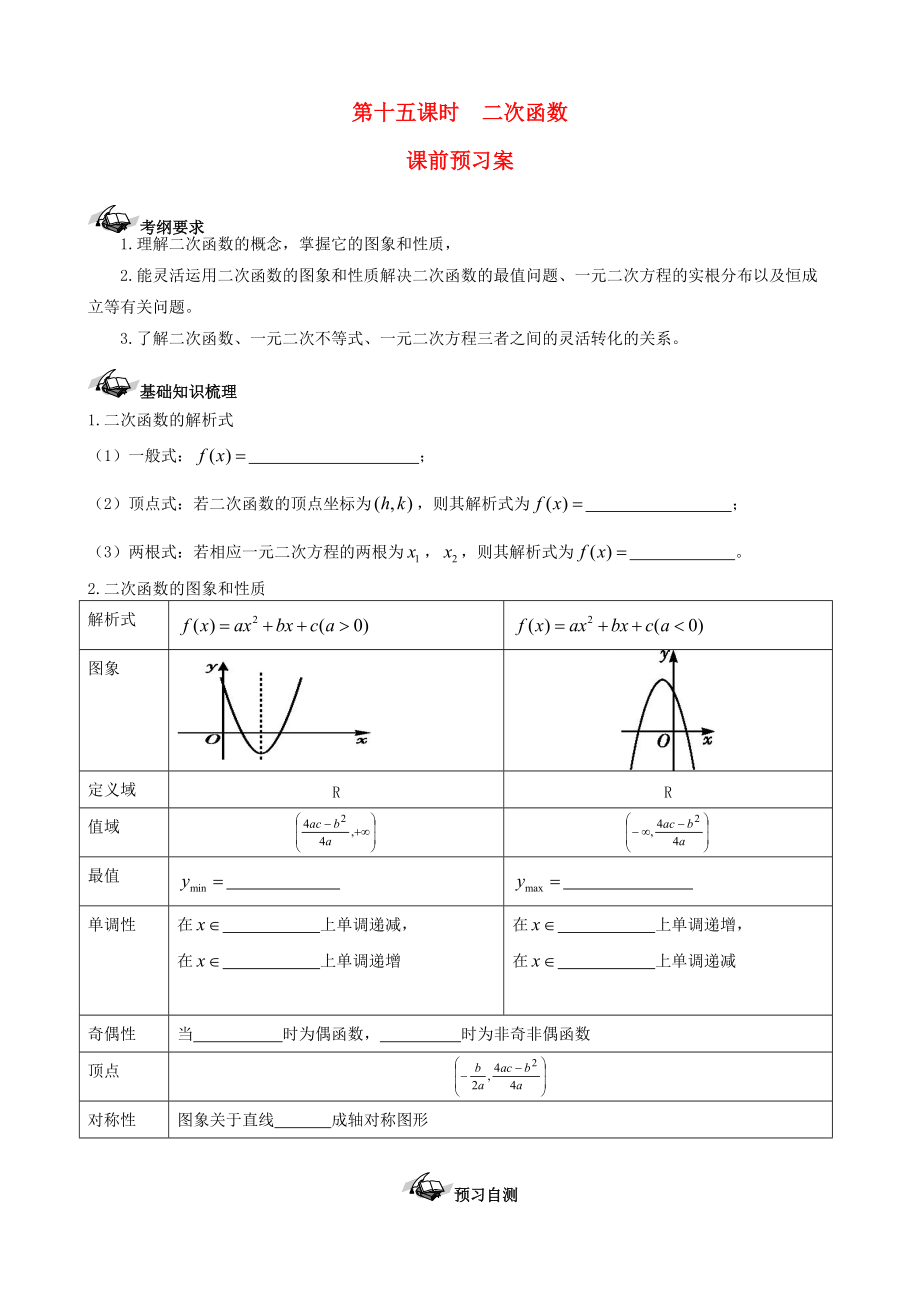
1、第十五課時(shí) 二次函數(shù) 課前預(yù)習(xí)案 考綱要求 1.理解二次函數(shù)的概念，掌握它的圖象和性質(zhì)， 2.能靈活運(yùn)用二次函數(shù)的圖象和性質(zhì)解決二次函數(shù)的最值問題、一元二次方程的實(shí)根分布以及恒成立等有關(guān)問題。 3.了解二次函數(shù)、一元二次不等式、一元二次方程三者之間的靈活轉(zhuǎn)化的關(guān)系。 基礎(chǔ)知識(shí)梳理 1.二次函數(shù)的解析式 （1）一般式： ； （2）頂點(diǎn)式：若二次函數(shù)的頂點(diǎn)坐標(biāo)為，則其解析式為 ； （3）兩根式：若相應(yīng)一元二次方程的兩根為，，則其解析式為 。 2.二次函數(shù)的圖象和性

2、質(zhì) 解析式 圖象 定義域 R R 值域 最值 單調(diào)性 在 上單調(diào)遞減， 在 上單調(diào)遞增 在 上單調(diào)遞增， 在 上單調(diào)遞減 奇偶性 當(dāng) 時(shí)為偶函數(shù)， 時(shí)為非奇非偶函數(shù) 頂點(diǎn) 對稱性 圖象關(guān)于直線 成軸對稱圖形 預(yù)習(xí)自測 1.方程的解是 ． 2.（2011福建文6）若關(guān)于的方程有兩個(gè)不相等的實(shí)數(shù)根，

3、則實(shí)數(shù)的取值范圍是（ ） A． B． C． D． 3.拋物線與軸交點(diǎn)的個(gè)數(shù)為（ ） A．0 B．1 C．2 D．以上都不對 4.拋物線，對稱軸為，且經(jīng)過點(diǎn)，則的值為（ ） A． B．0 C．1 D．3 5.若函數(shù)在上是減函數(shù)，則的取值范圍是（ ） A． B． C． D． 課堂探究案 典型例題 考點(diǎn)1 求二次函數(shù)的解析式 【典例1】（課本題再現(xiàn)）已知一個(gè)二次函數(shù)，，又知當(dāng)或時(shí)，這個(gè)函數(shù)的值都為0，則這個(gè)二次函數(shù)的解析式為 ． 【變式1】（課本題再現(xiàn)）已知一個(gè)二次函數(shù)的圖象的頂點(diǎn)是，與軸的一個(gè)交點(diǎn)為

4、，則這個(gè)二次函數(shù)的解析式為 ． 考點(diǎn)2 二次函數(shù)在給定區(qū)間上的最值問題 【典例2】求函數(shù)在上的值域． 【變式2】已知函數(shù)，． （1）當(dāng)時(shí)，求函數(shù)的最大值和最小值； （2）求實(shí)數(shù)的取值范圍，使在區(qū)間上是單調(diào)函數(shù)． 考點(diǎn)3 一元二次方程根的分布問題 【典例3】方程有兩個(gè)根，且一個(gè)大于1，一個(gè)小于1，求實(shí)數(shù)的取值范圍． 【變式3】（1）已知有且只有一根在區(qū)間內(nèi)，則實(shí)數(shù)的取值范圍是 ． （2）（2011重慶理）設(shè)、為整數(shù)，方程在區(qū)間內(nèi)有兩個(gè)不同的根，則的最小值為（ ） A． B．8 C．12 D．13

5、 考點(diǎn)4 二次函數(shù)的綜合應(yīng)用 【典例4】若二次函數(shù)，滿足，且． （1）求的解析式； （2）若在區(qū)間上，不等式恒成立，求實(shí)數(shù)的取值范圍． 【變式4】已知，若不等式的解集為，求，的值． 小結(jié)： 1.二次函數(shù)的圖象形狀、對稱軸、開口方向等是處理二次函數(shù)問題的重要依據(jù)． 2.二次函數(shù)在閉區(qū)間上，必有最大值和最小值，當(dāng)含有參數(shù)時(shí)，須對參數(shù)分區(qū)間討論． 3.二次方程根的分布問題，可借助二次函數(shù)圖象列不等式組求解． 4.三個(gè)二次問題（二次函數(shù)、二次方程、二次不等式）是中學(xué)數(shù)學(xué)中基礎(chǔ)問題，以函數(shù)為核心，三者密切相連． 當(dāng)堂檢測 1.已知點(diǎn)，，若點(diǎn)在函數(shù)的圖象上，則使得△

6、的面積為2的點(diǎn)的個(gè)數(shù)為（ ） A．4 B．3 C．2 D．1 2.一元二次方程（）有一個(gè)正根和一個(gè)負(fù)根的充分不必要條件是（ ） A． B． C． D． 3.若函數(shù)，則 ． 課后拓展案 A組全員必做題 1.若函數(shù)的定義域?yàn)?，值域?yàn)?，則的取值范圍是（ ） A． B． C． D． 2.設(shè)，是關(guān)于的方程的兩個(gè)實(shí)根，則的最小值是（ ） A． B．18 C．8 D．無最小值 3.二次函數(shù)的圖象與軸的兩個(gè)交點(diǎn)分別在開區(qū)間和內(nèi)，則實(shí)數(shù)的取值范圍是 ． 4.（課本題再現(xiàn)）已知函數(shù)在區(qū)間上有最大值3，最

7、小值2，則的取值范圍是 ． 5.若關(guān)于的方程的兩個(gè)實(shí)根，滿足，則實(shí)數(shù)的取值范圍是 ． 6.若是二次函數(shù)，則 ． B組提高選做題 1.若二次函數(shù)的圖象經(jīng)過原點(diǎn)，則 ． 2.已知函數(shù)的圖象關(guān)于軸對稱，則 ． 3.已知函數(shù)的一個(gè)零點(diǎn)比1大，一個(gè)零點(diǎn)比1小，求實(shí)數(shù)的取值范圍． 參考答案 預(yù)習(xí)自測 1. 2.C 3.C 4.B 5.B 典型例題 【典例1】 【變式1】 【典例2】解：對稱軸． ∵，∴有以下三種情況： ①時(shí),；，此時(shí)值域?yàn)椋? ②時(shí)，；，此時(shí)值域?yàn)椋? ③時(shí)，，，此時(shí)值域?yàn)椋? 【變式2】解：（1）時(shí)，． ∴當(dāng)x時(shí)，；． （2）對稱軸為， ∴或，即或． 【典例3】解：，∴，即． 【變式3】（1）；（2）D 【典例4】解：（1），∴． ， ∴． ∴． （2）， ∴對恒成立， 令，則對稱軸為， ∴，故． 【變式4】解：由題意可知即解得 當(dāng)堂檢測 1.A 2.C 3. A組全員必做題 1.B 2.A 3. 4. 5. 6.2 B組提高選做題 1.2 2.或1 3.解：，∴， ∴，即， ∴．