2019年中考數(shù)學(xué)同步復(fù)習(xí)重點題型訓(xùn)練大題加練二

《2019年中考數(shù)學(xué)同步復(fù)習(xí)重點題型訓(xùn)練大題加練二》由會員分享，可在線閱讀，更多相關(guān)《2019年中考數(shù)學(xué)同步復(fù)習(xí)重點題型訓(xùn)練大題加練二（13頁珍藏版）》請在裝配圖網(wǎng)上搜索。

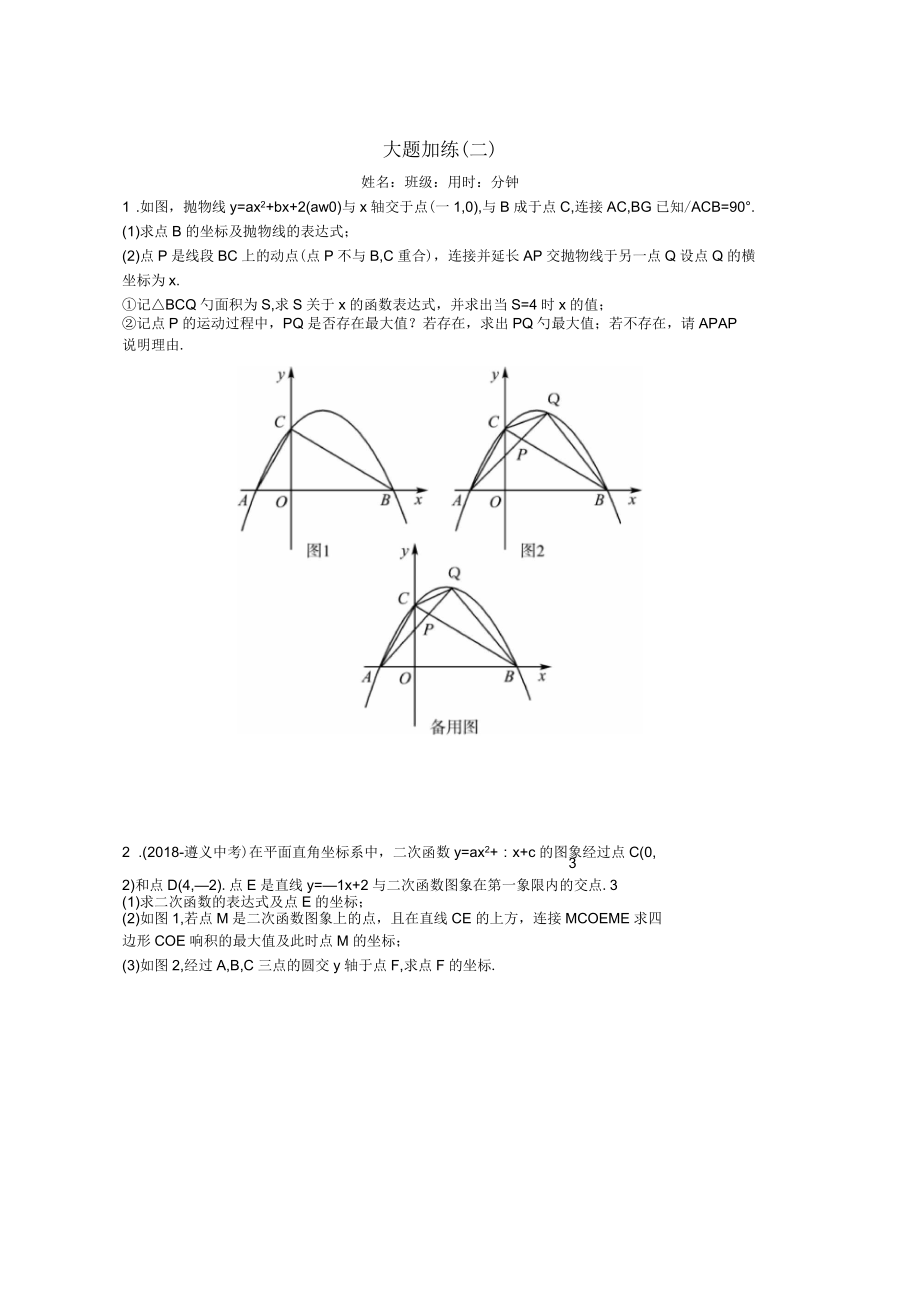
1、大題加練(二) 姓名：班級：用時：分鐘 1 .如圖，拋物線y=ax2+bx+2(aw0)與x軸交于點(一1,0),與B成于點C,連接AC,BG已知/ACB=90°. (1)求點B的坐標(biāo)及拋物線的表達式； (2)點P是線段BC上的動點(點P不與B,C重合)，連接并延長AP交拋物線于另一點Q設(shè)點Q的橫坐標(biāo)為x. ①記△BCQ勺面積為S,求S關(guān)于x的函數(shù)表達式，并求出當(dāng)S=4時x的值； ②記點P的運動過程中，PQ是否存在最大值？若存在，求出PQ勺最大值；若不存在，請APAP 說明理由. 2 .(2018-遵義中考)在平面直角坐標(biāo)系中，二次函數(shù)y=ax2+：x+c的圖象經(jīng)過點C

2、(0, 3 2)和點D(4,—2).點E是直線y=—1x+2與二次函數(shù)圖象在第一象限內(nèi)的交點.3 (1)求二次函數(shù)的表達式及點E的坐標(biāo)； (2)如圖1,若點M是二次函數(shù)圖象上的點，且在直線CE的上方，連接MCOEME求四 邊形COE響積的最大值及此時點M的坐標(biāo)； (3)如圖2,經(jīng)過A,B,C三點的圓交y軸于點F,求點F的坐標(biāo). 3 .如圖1,在平面直角坐標(biāo)系中，已知拋物線y=ax2+bx—5與x軸交于A(—1,0), B(5,0)兩點，與y軸相交于點C. (1)求拋物線的函數(shù)表達式； (2)如圖2,CE//x軸與拋物線相交于點E,點H是直線CE下方拋物線上的動點，

3、過點H且與y軸平行的直線與BGCE^別交于點F,G.試探究當(dāng)點H運動到何處時，四邊形CHEF的面積最大，求點H的坐標(biāo)； (3)若點K為拋物線的頂點，點M(4,m)是該拋物線上的一點，在x軸、y軸上分別找點 巳Q使四邊形PQKM勺周長最小，請求出點巳Q的坐標(biāo). 備用圖 4 .(2018?煙臺中考)如圖1,拋物線y=ax2+2x+c與x軸交于A(—4,0),B(1,0)兩 2 點，過點B的直線y=kx+j-分別與y軸及拋物線交于點C,D. (1)求直線和拋物線的表達式； (2)動點P從點O出發(fā)，在x軸的負半軸上以每秒1個單位長度的速度向左勻速運動.設(shè)運動時間為t秒，當(dāng)t為何

4、值時，△PDC為直角三角形？請直接寫出所有滿足條件的t的 值； ⑶如圖2,將直線BD沿y軸向下平移4個單位后，與x軸，y軸分別交于E,F兩點.在拋物線的對稱軸上是否存在點M,在直線EF上是否存在點N,使得D也MN的值最小？若 參考答案 1.解：(1)?./ACB=90,OCXAB, ???ZCO?90, ??.ZACO=ZCBQ/AOG=COB COAO △ACO^ACBQBOcd ??.Od=OA-OB. 當(dāng)x=0時，y=2,即C(0,2). -A(-1,0),C(0,2),.?.OB=4,B(4,0). 將A,B代入y=ax?+bx+2得 a—b+2=0

5、? 3 b = 一 2, {解得《 |16a+4b+2=0, 「?拋物線的表達式為 123cy=-2X+2x+2? (2)①如圖，連接OQ. 13 設(shè)點Q的坐標(biāo)為(x,--x 1 1 2 3 1 2 - S= SaoccH- Saobq— Saobc7= 5*2乂+]*4( — ~X + ]X + 2) — " X 2 X 4 = — x + 4x. 令一 x?+4x=4,解得xi= X2 = 2,故x的值為2. ②存在. 如圖，過點 Q作QHLBC于H. +-x+2), ZACF^ZQHR=9

6、0,ZAPG=ZQPH ?.△APSAQPFH PQQHQH AP 麗—5. QH=5QH QV PQs12.1 AP=5=5(—x+4x)=—5(x—MH= - fmi + |mT+ 2-( 3 3 +5 ，當(dāng)x=2時，A取得最大值，最大值為5. 2.解：（1）把C（0,2）,D（4,一2）代入二次函數(shù)表達式得 _2 解得$一3’ 9=2, c=2, 一?二次函數(shù)的表達式為丫=-3*2+萬+2, 33 11 y=—3+2, 聯(lián)立一次函數(shù)表達式得」 y=-qX2+-x+2, 33 解得x=0（舍去）或x=3,則E（3,1）

7、. （2）如圖，過M作MH//y軸，交CE于點H. 設(shè)M(mT,-|m2+|mi+2),則H(m,—；mi+2), 333 —gm^2)=—3m+2mx S四邊形 COEMF cc11 S/\OCE-FSacm^-X2X3+-MH- 3=—m2+3m+3, b321一3 當(dāng)m=—w=2時，S最大―此時M坐標(biāo)為（2，3）. ⑶如圖，連接BF. 當(dāng)—2x2+5x+2=0時，*2=二， 3344 回年,。氏年. 44 ???/ACQ=/ABF,/AOC=/FOB .AO6△FOB 在-5 ???QA=QC

8、即^=4, OFOBOF/+5 ^~4 -，r3 解得OF=一.3 則F坐標(biāo)為(0,-2). 3.解：(1)把A(—1,0),B(5,0)代入y=ax2+bx—5得 0=a—b—5, 0=25a+5b-5, a=1,解得M b=-4. ，二次函數(shù)的表達式為y=x2-4x-5(2)設(shè)H(t,t2-4t-5). ?.CE//x軸, 5=x2—4x—5, 解得xi=0,x2=4, E(4,—5),CE=4. 設(shè)直線BC的表達式為y2=a2x+b2. .B(5,0),C(0,—5), ：0=5a2+b2, ..—5=b2, =1[b2=—5, ，直線BC的表達

9、式為y2=x—5, 25225 ?.F(t,t—5),HF=t-5-(t-4t-5)=-(t—引+彳 .CE//x軸,HF//y軸, ???C吐EF, 15225 二?S四邊形chef=2CE，HF=-2(t—2)+—,??Hg,-% ⑶如圖，分另1J作K,M關(guān)于x軸，y軸對稱的點K',M',分別交PQ延長線于點K', M' W ???點K為頂點，，K(2,—9), ???點K關(guān)于y軸的對稱點K'的坐標(biāo)為(—2,—9). M(4,m),M(4,—5). ???點M關(guān)于x軸的對稱點M的坐標(biāo)為(4,5).設(shè)直線K'M'的表達式為y3=a3x+bs, -9=-2a

10、3+b3,則S 15=4a3+b3, 7 a3=3, 13b3=--, 3 「?直線KM的表達式為y3=-x——,33 易知圖中點P,Q即為符合條件的點, ??.P,Q的坐標(biāo)分別為P(13,0),Q(0,—±3).73 “一，2，， 4.解：（1）二.直線y=kx+a過點B（1,0）, 3 ?1-0=k+f,k=-1, 33 ，直線的表達式為y=—,x+133 0), B(1, 0), :拋物線y=ax2+2x+c與x軸交于A（—4, 0= 16a —8+c 0=a+ 2+ c, 解得 a=3, 「?拋物線的表達式為 2 2 8 y= -x

11、+ 2x --. 3 3 3 (2)t =9 s, 23 s, 9 3 15—木29 提示：情況一: DCP為直角時, 在 RtAOCB^, CB= 2 13 (3)2+12 =: 3 .'13 13 . 1cos/CBO=-^=13 "V BCcos/CBO=cos/CBP=1,PB 13 33'13 PB=13 13而3, ???點P的坐標(biāo)為（一"9,0）,9 時 S 4-9 △PDC^直角三角形. 可彳導(dǎo)D點坐標(biāo)為（ — 5, 4）. 當(dāng)/CDP為直角時，同理可得COS/CBP=BD=綽3

12、. BP13 BD=[62+42=2^/13, ?.BP=穿，..P點坐標(biāo)為（一穿，0） 33 ?.t=yS時，△PDC^直角三角形. 情況三：當(dāng)/DPC為直角時，設(shè)點P的坐標(biāo)為（a,0）,則 dF+C^=cD,即（a+5）2+42+a2+（2）2=52+（10）2,33 —15±V129 解得a=——m,6 .“點坐標(biāo)為（/叵，0）或（八座，。），66 ??.t=”二爛9s或正浮s時，APDa直角三角形. 66 （3）存在. 直線EF的表達式為y=—-|x+-|—4=—|x—47.3333 取D關(guān)于對稱軸的對稱點D',則D'坐標(biāo)為（2,4）. 如圖，過D'彳D

13、N±EF于點N,過點D'彳DG,x軸，垂足為Q,延長線交EF于點G. 設(shè)點N的坐標(biāo)為(a,-fa--^).33 ???/EQG=/D'NG=90°,ZG=ZG, ?./NDG=/GEB. ?./GEB=/ABC ?./ND'G^=AABC 則—— 4 一 2—a2 ???點N到 DG的距離為 2—(—2)=4, 又???對稱軸與 DG的距離為 37 2-(-2)=], ???點N在對稱軸的左側(cè)，由此可證明線段D' N與對稱軸有交點，其交點即為 小值時M的位置. 將x=2代入

14、y=—1x—J得y 33 14 3' .??點G的坐標(biāo)為（2, 14 -P D' 26 G=3 2\/i3, 261 ??.D'N=D'G-cos/NDG=D'G-cosZABC=-- 3_J3 即DMbMN的最小值為2.13. 3…2,2 設(shè)點M的坐標(biāo)為（一1b）,則一4—^一=tan/NDG=3, 解得b=—4, 35 .??點m的坐標(biāo)為（一萬，一彳）. .............35 綜上所述，D也MN的最小值為2d13,點M的坐標(biāo)為（一萬，一N，點N的坐標(biāo)為（一2,— 2）. -210—=tan/NDG=tan/ABC=-, 一-a——) 33 解得a=-2, 210 —5”三一*2, .??點N的坐標(biāo)為（—2,—2）.