《江蘇省南京市2010高三應(yīng)知應(yīng)會講義 平面向量與復(fù)數(shù)教案 蘇教版》由會員分享，可在線閱讀，更多相關(guān)《江蘇省南京市2010高三應(yīng)知應(yīng)會講義 平面向量與復(fù)數(shù)教案 蘇教版（2頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、平面向量與復(fù)數(shù)
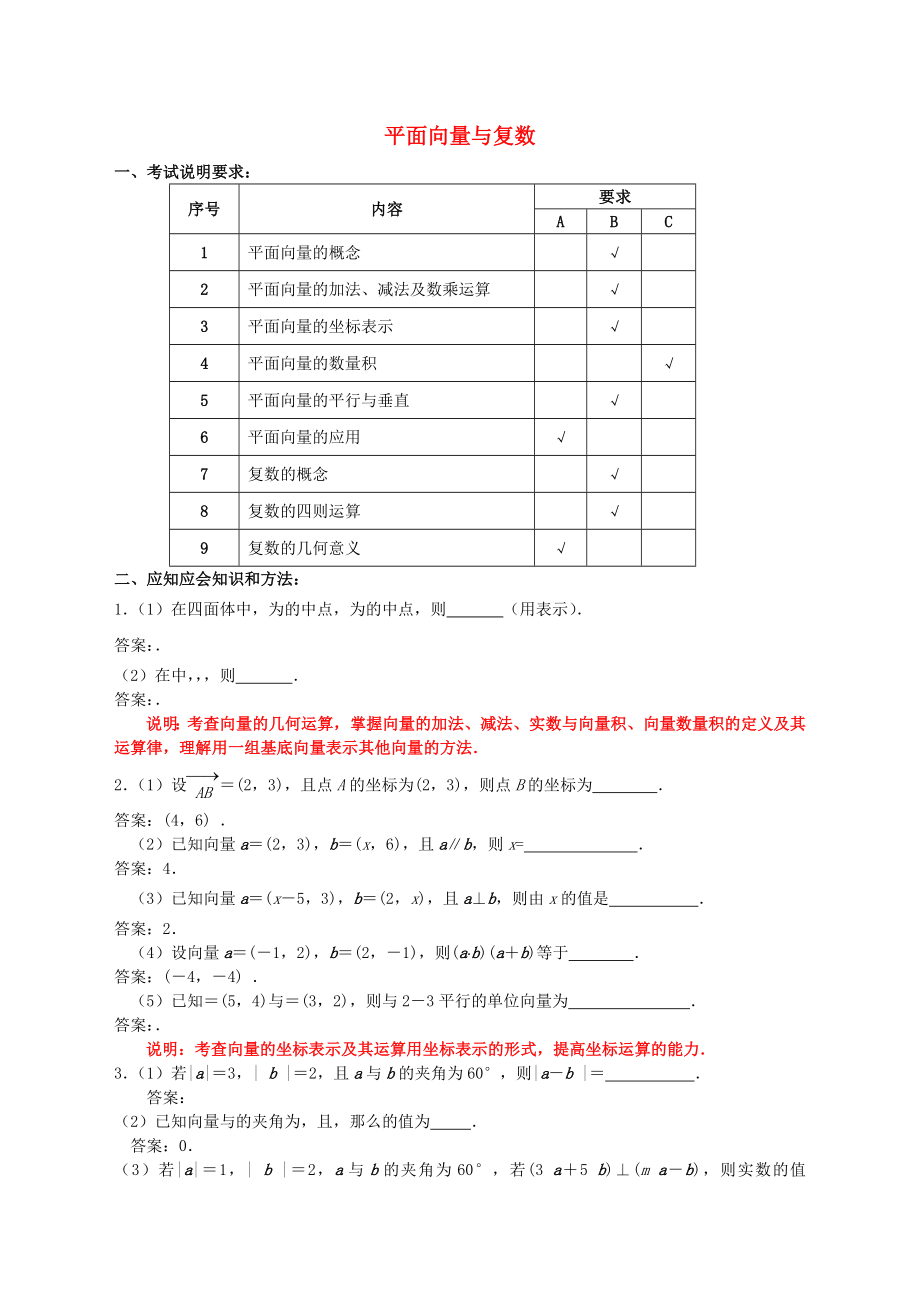
一、考試說明要求：ww w.ks 5u.co m
序號
內(nèi)容
要求
A
B
C
1
平面向量的概念
√
2
平面向量的加法、減法及數(shù)乘運算
√
3
平面向量的坐標(biāo)表示
√
4
平面向量的數(shù)量積
√
5
平面向量的平行與垂直
√
6
平面向量的應(yīng)用
√
7
復(fù)數(shù)的概念
√
8
復(fù)數(shù)的四則運算
√
9
復(fù)數(shù)的幾何意義
√
二、應(yīng)知應(yīng)會知識和方法：
1．（1）在四面體中，為的中點，為的中點，則 （用表示）．
答案：．
（
2、2）在中，，，則 ．
答案：．
說明：考查向量的幾何運算，掌握向量的加法、減法、實數(shù)與向量積、向量數(shù)量積的定義及其運算律，理解用一組基底向量表示其他向量的方法．
2．（1）設(shè)＝(2，3)，且點A的坐標(biāo)為(2，3)，則點B的坐標(biāo)為 ．
答案：(4，6) ．
（2）已知向量a＝(2，3)，b＝(x，6)，且a∥b，則x= ．
答案：4．
（3）已知向量a＝(x－5，3)，b＝(2，x)，且a⊥b，則由x的值是 ．
答案：2．
（4）設(shè)向量a＝(－1，2)，b＝(2，－1)，則(a×b)(a＋b)等于
3、 ．
答案：(－4，－4) ．
（5）已知＝(5，4)與＝(3，2)，則與2－3平行的單位向量為 ．
答案：．
說明：考查向量的坐標(biāo)表示及其運算用坐標(biāo)表示的形式，提高坐標(biāo)運算的能力．
3．（1）若|a|＝3，| b |＝2，且a與b的夾角為60°，則|a－b |＝ ．
答案： ww w.ks 5u.co m
（2）已知向量與的夾角為，且，那么的值為 ．
答案：0．
（3）若|a|＝1，| b |＝2，a與b的夾角為60°，若(3 a＋5 b)⊥(m a－b)，則實數(shù)的值為 ．
答案：
（4）已知平面上
4、三點A，B，C滿足|AB|=5，|BC|=6，|CA|=7，則×＋×＋×的值等于 ．
答案：－55．
（5）在△ABC中，O為中線AM上一個動點，若AM=2，則×(＋)的最小值是__________．
答案：－2．
說明：考查向量的模、夾角、平行、垂直的坐標(biāo)表示方法，要記準(zhǔn)公式，確保運算結(jié)果正確．平面向量的模的問題常常用來轉(zhuǎn)化；兩個平面向量的夾角常常通過來求解．
4．（1）已知，，，點在線段上，且，則 的值是________________．ww w.ks 5u.co m
A
B
C
D
M
N
O
答案：
（2）如圖，AB是半圓O的直徑，C，D是弧A
5、B的三等分點，
M，N是線段AB的三等分點．若OA=6，則的
值是 ．
答案：26．
（3）已知△ABC中，AB=3，AC=2，D是BC邊上的中點，則 ．
答案：．ww w.ks 5u.co m
（4）已知△ABC中，AB=3，AC=2，O是△ABC外接圓的圓心，則 ．
答案：．
說明：著重考查向量數(shù)量積．兩向量的數(shù)量積常常通過以下三種途徑加以計算：（1）利用定義，即求出兩個向量的模及其夾角；（2）建立適當(dāng)?shù)淖鴺?biāo)系利用坐標(biāo)；（3）利用平面向量基本定理轉(zhuǎn)化為基底之間的運算．三角形中的有關(guān)性質(zhì)要能進行熟練轉(zhuǎn)換．
5．（1）復(fù)數(shù)的實部是 ．
答案：2．
（2）復(fù)數(shù)在復(fù)平面內(nèi)對應(yīng)點到原點的距離為 ．
答案：2．ww w.ks 5u.co m
（3）是虛數(shù)單位， ?。ㄓ玫男问奖硎荆?
答案：．
（4）若復(fù)數(shù)是純虛數(shù)(是虛數(shù)單位，是實數(shù))，則 ?。?
答案：2．
說明：考查復(fù)數(shù)的有關(guān)概念：復(fù)數(shù)、虛數(shù)、純虛數(shù)、實數(shù)、虛部、實部等；掌握復(fù)數(shù)的四則運算；了解復(fù)數(shù)的幾何意義．
江蘇省南京市2010高三應(yīng)知應(yīng)會講義 平面向量與復(fù)數(shù)教案 蘇教版
