《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第17講 解直角三角形》由會員分享,可在線閱讀�����,更多相關(guān)《陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第17講 解直角三角形(2頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索����。
1、第17講 解直角三角形
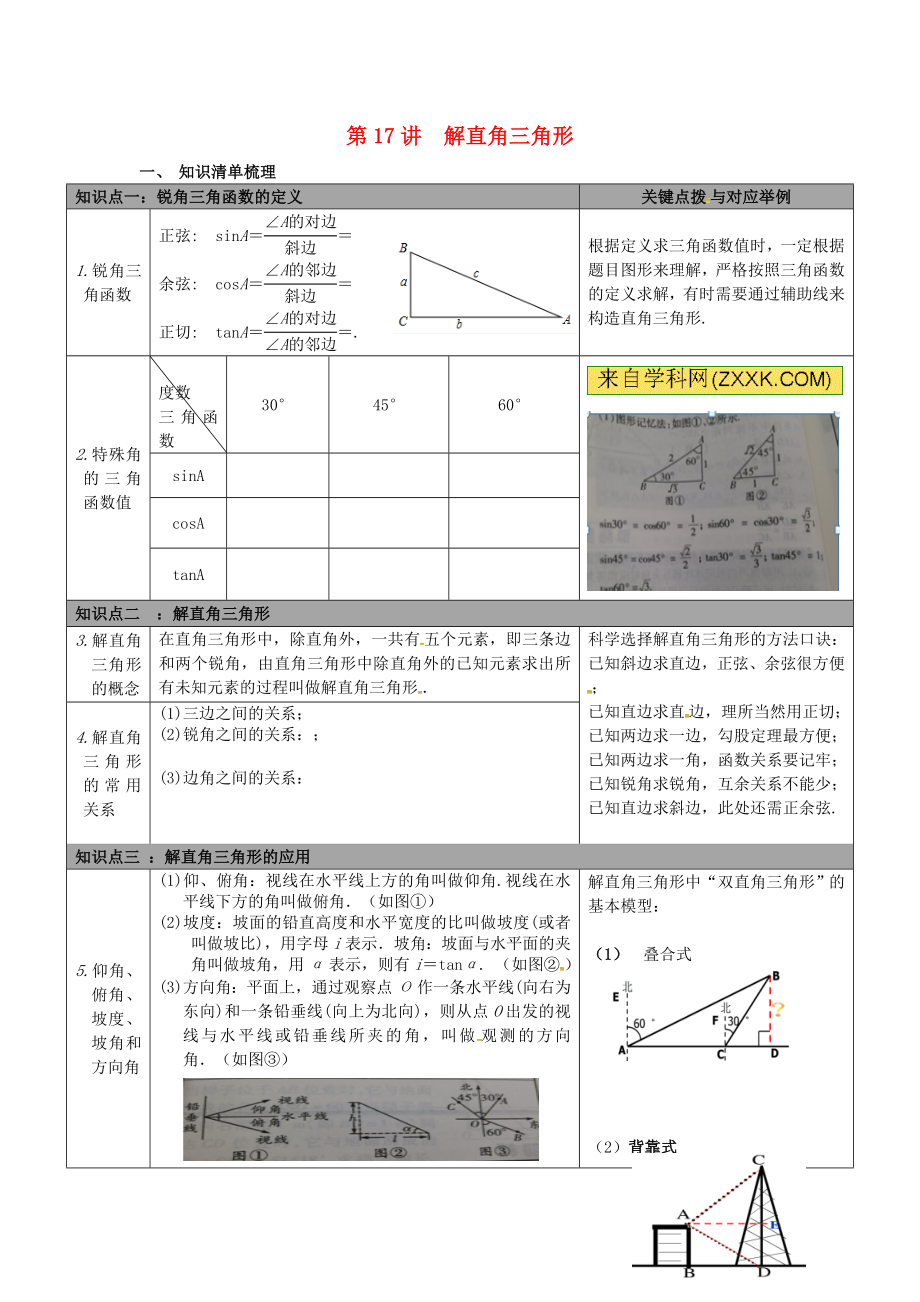
一�����、 知識清單梳理
知識點(diǎn)一:銳角三角函數(shù)的定義
關(guān)鍵點(diǎn)撥與對應(yīng)舉例
1.銳角三角函數(shù)
正弦: sinA==
余弦: cosA==
正切: tanA==.
根據(jù)定義求三角函數(shù)值時(shí)��,一定根據(jù)題目圖形來理解�,嚴(yán)格按照三角函數(shù)的定義求解,有時(shí)需要通過輔助線來構(gòu)造直角三角形.
2.特殊角的三角函數(shù)值
度數(shù)
三角函數(shù)
30°
45°
60°
sinA
cosA
tanA
知識點(diǎn)二 :解直角三角形
3.解直角三角形的概念
在直角三角形中���,除直角
2�、外�,一共有五個(gè)元素��,即三條邊和兩個(gè)銳角���,由直角三角形中除直角外的已知元素求出所有未知元素的過程叫做解直角三角形.
科學(xué)選擇解直角三角形的方法口訣:
已知斜邊求直邊,正弦�����、余弦很方便����;
已知直邊求直邊,理所當(dāng)然用正切���;
已知兩邊求一邊�,勾股定理最方便��;
已知兩邊求一角��,函數(shù)關(guān)系要記牢�;
已知銳角求銳角����,互余關(guān)系不能少;
已知直邊求斜邊,此處還需正余弦.
4.解直角三角形的常用關(guān)系
(1)三邊之間的關(guān)系�����;
(2)銳角之間的關(guān)系:��;
(3)邊角之間的關(guān)系:
知識點(diǎn)三 :解直角三角形的應(yīng)用
5.仰角��、俯角�、坡度、坡角和方向角
(1)仰��、俯角:視線在水平線上方的
3����、角叫做仰角.視線在水平線下方的角叫做俯角.(如圖①)
(2)坡度:坡面的鉛直高度和水平寬度的比叫做坡度(或者叫做坡比),用字母i表示. 坡角:坡面與水平面的夾角叫做坡角����,用α表示,則有i=tanα. (如圖②)
(3)方向角:平面上��,通過觀察點(diǎn)Ο作一條水平線(向右為東向)和一條鉛垂線(向上為北向)����,則從點(diǎn)O出發(fā)的視線與水平線或鉛垂線所夾的角���,叫做觀測的方向角.(如圖③)
解直角三角形中“雙直角三角形”的基本模型:
(1) 疊合式
(2)背靠式
解題方法:這兩種模型種都有一條公共的直角邊,解題時(shí)��,往往通過這條邊為中介在兩個(gè)
4�����、三角形中依次求邊�����,或通過公共邊相等�����,列方程求解.
6.解直角三角形實(shí)際應(yīng)用的一般步驟
(1)弄清題中名詞���、術(shù)語�,根據(jù)題意畫出圖形��,建立數(shù)學(xué)模型���;
(2)將條件轉(zhuǎn)化為幾何圖形中的邊�、角或它們之間的關(guān)系����,把實(shí)際問題轉(zhuǎn)化為解直角三角形問題;
(3)選擇合適的邊角關(guān)系式���,使運(yùn)算簡便��、準(zhǔn)確�����;
(4)得出數(shù)學(xué)問題的答案并檢驗(yàn)答案是否符合實(shí)際意義�����,從而得到問題的解.
二����、 典例試做:
1����、“村村通”公路工程拉近了城鄉(xiāng)距離,加速了我區(qū)農(nóng)村經(jīng)濟(jì)建設(shè)步伐.如圖所示�����,C村村民欲修建一條水泥公路,將C村與區(qū)級公路相連.在公路A處測得C村在北偏東60°方向�,沿區(qū)級公路前進(jìn)500m,在B處測得C村在北偏東30°方向.為節(jié)約資源�����,要求所修公路長度最短.畫出符合條件的公路示意圖�,并求出公路長度.(結(jié)果保留整數(shù))
2、某數(shù)學(xué)興趣小組的同學(xué)在一次數(shù)學(xué)活動中���,為了測量某建筑物AB的高�,他們來到與建筑物AB在同一平地且相距12m的建筑物CD上的C處觀察���,測得此建筑物頂部A的仰角為30°��、底部B的俯角為45°.求建筑物AB的高(精確到1m��,可供選用的數(shù)據(jù):≈1.4��,≈1.7).
 陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第17講 解直角三角形
陜西省山陽縣色河鋪鎮(zhèn)2018年中考數(shù)學(xué)總復(fù)習(xí) 第17講 解直角三角形