2022屆高考數(shù)學(xué)二輪復(fù)習(xí) 小題標(biāo)準(zhǔn)練（一）文

《2022屆高考數(shù)學(xué)二輪復(fù)習(xí) 小題標(biāo)準(zhǔn)練（一）文》由會員分享，可在線閱讀，更多相關(guān)《2022屆高考數(shù)學(xué)二輪復(fù)習(xí) 小題標(biāo)準(zhǔn)練（一）文（7頁珍藏版）》請在裝配圖網(wǎng)上搜索。

1、2022屆高考數(shù)學(xué)二輪復(fù)習(xí) 小題標(biāo)準(zhǔn)練（一）文 一、選擇題(本大題共12小題,每小題5分,共60分.在每小題給出的四個選項(xiàng)中,只有一項(xiàng)是符合題目要求的) 1.已知集合P={x∈R|01},所以RQ ?RP. 2.設(shè)z=a+bi(a,b∈R,i為虛數(shù)單位),若(1+i)2+|2i|=,則直線bx-ay+

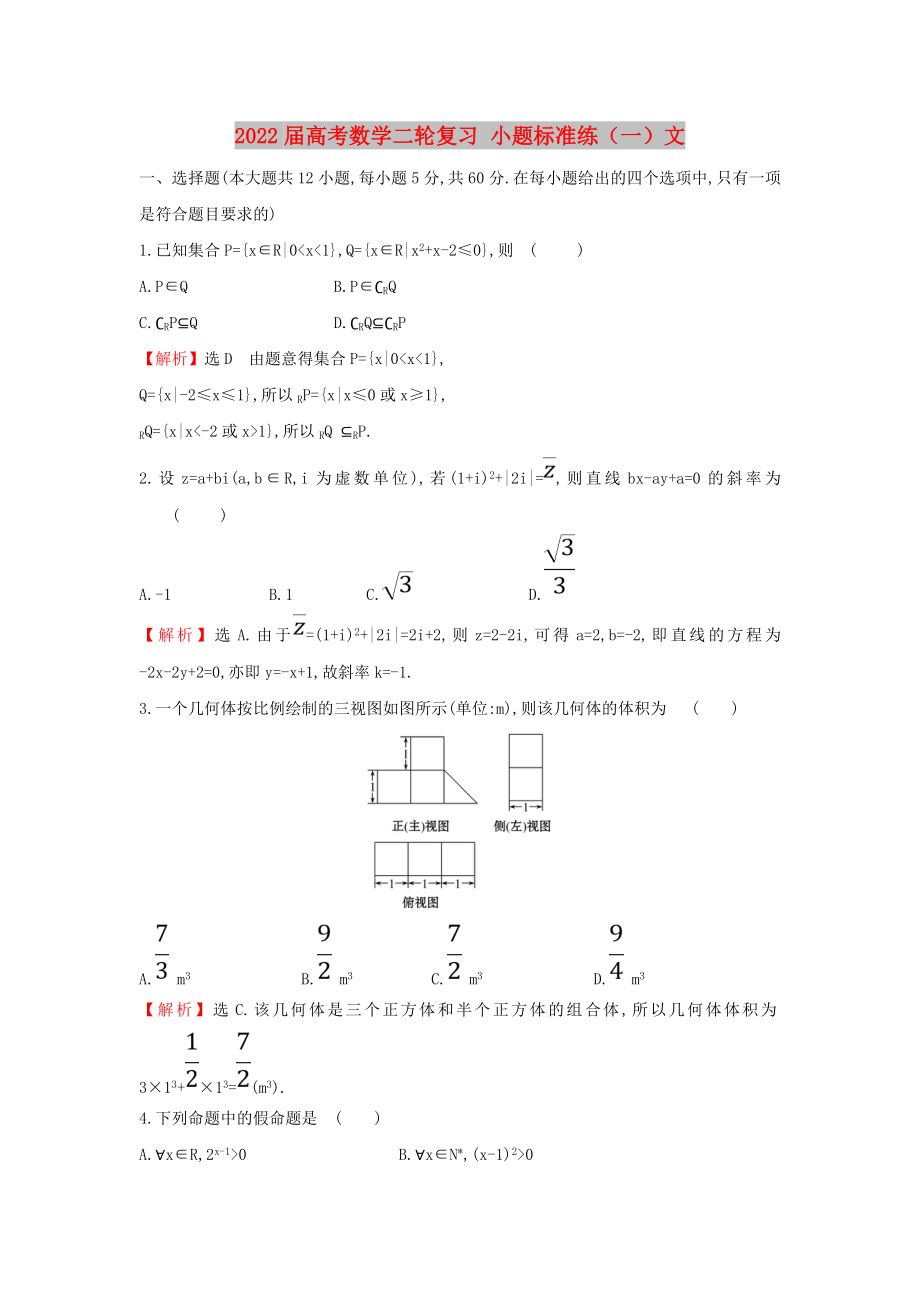
2、a=0的斜率為 (　　 ) A.-1 B.1 C. D. 【解析】選A.由于=(1+i)2+|2i|=2i+2,則z=2-2i,可得a=2,b=-2,即直線的方程為-2x-2y+2=0,亦即y=-x+1,故斜率k=-1. 3.一個幾何體按比例繪制的三視圖如圖所示(單位:m),則該幾何體的體積為 (　　) A. m3 B. m3 C. m3 D. m3 【解析】選C.該幾何體是三個正方體和半個正方體的組合體,所以幾何體體積為3×13+×13=(m3). 4.下列命題中的假命題是 (　　) A.?x∈R,2x-1>0 B.?x∈N*,(x-1

3、)2>0 C.?x0∈R,ln x0<1 D.?x0∈R,tan x0=2 【解析】選B.因?yàn)?x-1>0對?x∈R恒成立,所以A是真命題,當(dāng)x=1時,(x-1)2=0,所以B是假命題. 5.已知<α<,sin(α-)=,則cos α= (　　) A. B.- C. D.- 【解析】選B.方法一:因?yàn)?α<,所以α-∈(0,), 又sin(α-)=, 所以cos(α-)==. 所以cos α=cos[(α-)+]=cos(α-)cos-sin(α-)sin=(-)=-. 方法二:因?yàn)閟in(α-)=, 所以(sin α-cos α)=, 即sin α-

4、cos α=①,又<α<, 所以sin α>|cos α|. 所以sin α+cos α==②,由得cos α=-. 6.已知實(shí)數(shù)x,y滿足不等式組 若z=x-y,則z的最大值為 (　　) A.3　 B.4 C.5　 D.6 【解析】選A.作出不等式組 所對應(yīng)的可行域(如圖所示),變形目標(biāo)函數(shù)為y=x-z,平移直線y=x-z可知,當(dāng)直線經(jīng)過點(diǎn)(3,0)時,z取最大值,代值計算可得z=x-y的最大值為3. 7.已知數(shù)列{an}的前n項(xiàng)和Sn=n2-6n,則{|an|}的前n項(xiàng)和Tn= (　　) A.6n-n2 B.n2-6n+18 C. D. 【

5、解析】選C.由Sn=n2-6n可得,當(dāng)n≥2時,an=Sn-Sn-1=n2-6n-(n-1)2+6(n-1)=2n-7.當(dāng)n=1時,S1=-5=a1,也滿足上式,所以an=2n-7,n∈N*. 所以n≤3時,an<0;n>3時,an>0,當(dāng)n≤3時, Tn=-Sn=6n-n2, 當(dāng)n>3時,Tn=-a1-a2-a3+a4+…+an =Sn-2S3 =n2-6n-2(32-6×3) =n2-6n+18, 所以Tn= 8.如圖在邊長為1的正方形組成的網(wǎng)格中,平行四邊形ABCD的頂點(diǎn)D被陰影遮住,請找出D的位置,計算·的值為 (　　) A.10 B.11 C.12 D.

6、13 【解析】選B.如圖建立平面直角坐標(biāo)系,則·=·=(4,1)·(2,3)=11. 9.在△ABC中,AC=,BC=2,B=,過B作AC的垂線,垂足為D,則 (　　) A.=+ B.=+ C.=+ D.=+ 【解析】選A.由余弦定理得c2+22-2c×2×cos =()2,解得c=3,因?yàn)锽D是 △ABC的高,所以×BD=×2×3×sin ,解得BD=,由余弦定理得 cos C==,所以CD=2×=,所以=,所以-=(-),所以=+. 10.設(shè)數(shù)列{an}的前n項(xiàng)和為Sn,且滿足an+Sn=1,則Sn的取值范圍是 (　　) A.(0,1)　

7、B.(0,+∞) C. D. 【解析】選C.已知an+Sn=1,當(dāng)n=1時,得a1=;當(dāng)n≥2時,an-1+Sn-1=1,兩式相減,得an-an-1+an=0,2an=an-1,由題意知,an-1≠0,所以=(n≥2), 所以數(shù)列{an}是首項(xiàng)為,公比為的等比數(shù)列,所以Sn==1-,所以 Sn∈. 11.設(shè)拋物線y2=4x的準(zhǔn)線為l,點(diǎn)M在拋物線上,且在第一象限內(nèi),若圓M與l相切,在y軸上截得的線段長為6,則圓M的標(biāo)準(zhǔn)方程為 (　　) A.(x-4)2+(y-4)2=5 B.(x-3)2+(y-2)2=25 C.(x-4)2+(y-4)2=25 D.(x

8、-2)2+(y-3)2=5 【解析】選C.設(shè)圓M的半徑為r,圓心的坐標(biāo)為(a,b),a>0,b>0,因?yàn)閽佄锞€y2=4x的準(zhǔn)線為l,所以準(zhǔn)線l的方程為x=-1,因?yàn)閳AM與l相切,所以a=r-1,因?yàn)閳AM在y軸上截得的線段長為6,所以(r-1)2+32=r2,解得r=5,所以a=4,又b2=4a,所以b=4,所以圓M的標(biāo)準(zhǔn)方程為(x-4)2+(y-4)2=25. 12.定義域?yàn)镽的函數(shù)f(x)滿足f(x-2)=-f(x)且f(x)= ,則關(guān)于x的方程5 f(x)=x的實(shí)數(shù)解個數(shù)為 (　　) A.7 B.8 C.9 D.10 【解析】選B.因?yàn)閒 (x-2)=-f (x),所以

9、f(x-4)=-f(x-2)=f(x),所以f(x)的 周期為4. 由5f (x)=x得f(x)=,作出y=f(x)和y=的函數(shù)圖象如圖所示: 由圖象可知兩圖象有8個交點(diǎn),故關(guān)于x的方程5f(x)=x 有8個解. 二、填空題(本大題共4小題,每小題5分,共20分.請把正確答案填在題中橫線上) 13.以下四個命題中:①在回歸分析中,可用相關(guān)指數(shù)R2的值判斷模型的擬合效果,R2越大,模型的擬合效果越好;②兩個隨機(jī)變量的線性相關(guān)性越強(qiáng),相關(guān)系數(shù)的絕對值越接近于1;③若數(shù)據(jù)x1,x2,x3,…,xn的方差為1,則2x1,2x2,2x3,…,2xn的方差為2;④對分類變量x與y的隨機(jī)變量K

10、2的觀測值k來說,k越小,判斷“x與y有關(guān)系”的把握程度越大.其中真命題是____________.? 【解析】由相關(guān)指數(shù)R2越接近于1,模型的擬合效果越好知①正確;由相關(guān)系數(shù)r的絕對值越接近于1,兩個隨機(jī)變量的線性相關(guān)性越強(qiáng)知②正確;③④錯誤.故真命題是①②. 答案:①② 14.某農(nóng)戶計劃種植黃瓜和韭菜,種植面積不超過50畝,投入資金不超過54萬元,假設(shè)種植黃瓜和韭菜的產(chǎn)量、成本和售價如表: 年產(chǎn)量/畝 年種植成本/畝 每噸售價 黃瓜 4噸 1.2萬元 0.55萬元 韭菜 6噸 0.9萬元 0.3萬元 為使一年的種植總利潤(總利潤=總銷售收入-總種植成本)最

11、大,那么黃瓜和韭菜的種植面積(單位:畝)分別為____________.? 【解析】設(shè)種植黃瓜x畝,種植韭菜y畝,因此,原問題轉(zhuǎn)化為在條件下, 求z=0.55×4x+0.3×6y-1.2x-0.9y=x+0.9y的最大值.畫出可行域如圖.利用線性規(guī)劃知識可知, 當(dāng)x,y取的交點(diǎn)(30,20)時,z取得最大值. 答案:30,20 15.若函數(shù)f(x)=x2+a|x-2|在(0,+∞)上單調(diào)遞增,則實(shí)數(shù)a的取值范圍是________.? 【解析】因?yàn)閒(x)=x2+a|x-2|,所以f(x)= 又因?yàn)閒(x)在(0,+∞)上單調(diào)遞增, 所以 ?-4≤a≤0,即實(shí)數(shù)a的取值范圍是[-4

12、,0]. 答案:[-4,0] 16.設(shè)A={(x,y)|x2-a(2x+y)+4a2=0},B={(x,y)||y|≥b|x|},若對任意實(shí)數(shù)a,均有A?B成立,則實(shí)數(shù)b的最大值為____________.? 【解析】(1)當(dāng)b≤0時,集合B表示的是整個坐標(biāo)平面上的所有點(diǎn),顯然對任意實(shí)數(shù)a,均有A?B成立. (2)當(dāng)b>0時,集合B表示的是兩條直線y=±bx表示的上下對角區(qū)域,如圖所示,若a=0,則A={(x,y)|x=0},即集合A表示y軸上的所有點(diǎn),滿足A?B成立.若a≠0,由x2-a(2x+y)+4a2=0,得y=x2-2x+4a,則此拋物線與直線y=bx至多有一個公共點(diǎn),且與y=-bx至多有一個公共點(diǎn),即方程bx=x2-2x+4a,方程-bx=x2-2x+4a至多有一個解,即方程x2-(2a+ab)x+4a2=0,方程x2-(2a-ab)x+4a2=0至多有一個解,則解得-2≤b≤2.因?yàn)閎>0,所以0